2.变式训练,巩固垂线的概念和画法,如图根据下列语句画图:

　　 (1)过点P画射线MN的垂线,Q为垂足;

　　 (2)过点P画射线BN的垂线,交射线BN反向延长线于Q点;

(3)过点P画线段AB的垂线,交线AB延长线于Q点.

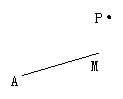
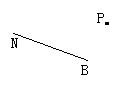
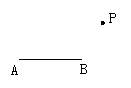
　　 学生画完图后,教师归结:画一条射线或线段的垂线, 就是画它们所在直线的垂线.

1.学生用三角尺或量角器画已知直线L的垂线.

　　 (1)已知直线L(教师在黑板上画一条直线L),画出直线L的垂线.待学生上黑板画出L的垂线后,教师追问学生:还能画出L的垂线吗?能画几条?通过师生交流, 使学生明确直线L的垂线有无数多条,即存在,但有不确定性.教师再问:怎样才能确定直线L的垂线位置?在学生道出:在直线L上取一点A,过点A画L的垂线,并且动手画出图形.

　　 教师板书学生的结论:经过直线上一点有且只有一条直线与已知直线垂直.

　　 (2)经过直线L外一点B画直线L的垂线,这样的垂线能画出几条?从中你又得出什么结论?

　　 教师板书学生的结论:经过直线外一点有且只有一条直线与已知直线垂直.

　　 教师让学生通过画图操作所得两条结论合并成一条,并板书:

　　 垂线性质1:过一点有且只有一条直线与已知直线垂直.

5.简单应用

　　 (1)学生观察课本P6图5.1-6中的一些互相垂直的线条, 并再举出生活中其他实例.

　　 (2)判断以下两条直线是否垂直:

　　 ①两条直线相交所成的四个角中有一个是直角;

　　 ②两条直线相交所成的四个角相等;

　　 ③两条直线相交,有一组邻补角相等;

　　 ④两条直线相交,对顶角互补.

4.垂直的表示法.

垂直用符号“⊥”来表示，结合课本图5.1－5说明“直线AB垂直于直线CD， 垂足为O”，则记为AB⊥CD,垂足为O，并在图中任意一个角处作上直角记号,如图.

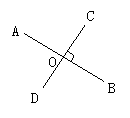
3.师生共同给出垂直定义.

　　 师生分清“互相垂直”与“垂线”的区别与联系：“互相垂直”指两条直线的位置关系；“垂线”是指其中一条直线对另一条直线的命名。 如果说两条直线“互相垂直”时，其中一条必定是另一条的“垂线”， 如果一条直线是另一条直线的“垂线”，则它们必定“互相垂直”。

2.教师出示相交线的模型,演示模型,学生观察思考:固定木条a,转动木条, 当b的位置变化时,a、b所成的角a是如何变化的?其中会有特殊情况出现吗?当这种情况出现时,a、b所成的四个角有什么特殊关系?

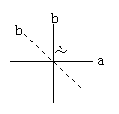
　　 教师在组织学生交流中,应学生明白:当b的位置变化时,角a从锐角变为钝角,其中∠a是直角是特殊情况.其特殊之处还在于:当∠a是直角时,它的邻补角,对顶角都是直角,即a、b所成的四个角都是直角,都相等.

1.学生观察教室里的课桌面、黑板面相邻的两条边, 方格纸的横线和竖线……,思考这些给大家什么印象?

　　 在学生回答之后,教师指出:“垂直”两个字对大家并不陌生, 但是垂直的意义,垂线有什么性质,我们不一定都了解,这可是我们要学习的内容.

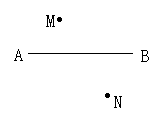
2001.杭州)如图7所示,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是　位于公路AB两侧的村庄,设汽车行驶到P点位置时,离村庄M最近,行驶到Q点位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.

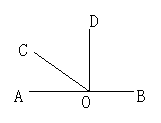
　　 如图6所示,O为直线AB上一点,∠AOC=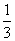∠BOC,OC是∠AOD的平分线.

　　 (1)求∠COD的度数;(2)判断OD与AB的位置关系,并说明理由.

如图所示,村庄A要从河流L引水入庄,

需修筑一水渠,请你画出修筑水渠的路线图.