
1、平面上三条直线相交,最多能有( )对对顶角
A.4 B.5 C.6 D.7
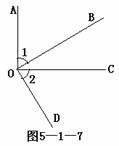
4、如图5-1-7,OA⊥OC,∠1=∠2,
则OB与OD的位置关系是
u 慧眼识金
3、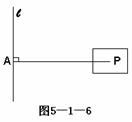 如图5-1-6,学校田径运动会上,裁判测量同学们的跳远成绩是看落在沙坑中的脚印P到起跳线l的距离,这种测量方法的根据是
如图5-1-6,学校田径运动会上,裁判测量同学们的跳远成绩是看落在沙坑中的脚印P到起跳线l的距离,这种测量方法的根据是
2、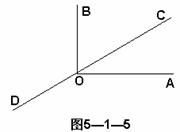 如图5-1-5,已知OA⊥OB,直线CD过点O,且∠AOC=35°,则∠BOD=
如图5-1-5,已知OA⊥OB,直线CD过点O,且∠AOC=35°,则∠BOD=
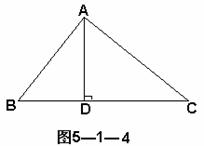
1、如图5-1-4,BA⊥AC于A,AD⊥BC于D,则图中点C到AB的距离是线段 的长,点B到AC的距离是线段 的长,与∠B相等的角是 ,与∠C相等的角是 。
5.1 相交线
趣味导读
你看过立交桥吗?你观察过教室和黑板相邻的两条边吗?这些都给我们以相交线的形象。其中还有特例--垂直。通过这节的探究,相信我们大家就能对这些概念和性质有更深入的理解,我们就能更好地应用其解决问题。
智能点拨
(例1)如图5-1-1,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数。
(1)若∠AOB=α,其他条件不变,求∠MON的度数。
(2)若∠BOC=β(β为锐角),其他条件不变,求∠MON的度数。
(3)从上面结果中能看出什么规律?
(4)线段的计算与角的计算存在着紧密联系,它们之间可以互相借鉴解法,请你模仿上述题设计一道以线段为背景的计算题,并写出其中的规律。

[点拨]由已知,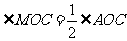 ,
,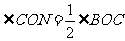
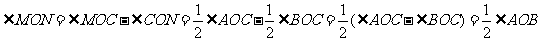
所以∠MON的大小总等于∠AOB的一半,而与锐角∠BOC的大小无关。
[答案]解: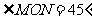
(1)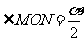 ; (2)
; (2)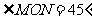 ;
;
(3)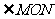 的大小总等于∠AOB的一半,而与锐角∠BOC的大小无关;
的大小总等于∠AOB的一半,而与锐角∠BOC的大小无关;
(4)涉及的问题为:如图5-1-2,已知线段AC,B为AC上一点,M、N分别为AB、BC的中点,求MN的长。本题的规律是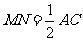 ,而与BC的长度无关。
,而与BC的长度无关。
(例题2)如图5-1-3,AB和CD相交于点O,OE是∠BOC的平分线,
且∠AOE=140°,求∠BOD的度数。
[点拨]可用邻补角或对顶角的性质求解。
[答案]解法一:由邻补角定义,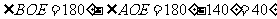 ,
,
由角平分线定义,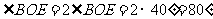 ,
,
由邻补角定义,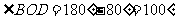
解法二: ,
,
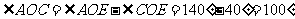
所以由对顶角性质得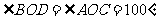
随堂反馈
u
 画龙点睛
画龙点睛
4. 1100 5. B 6. C 7 C 8. C
快乐晋级: 9. 1200 600 1200 600 10. 360 11.800 12
(1)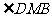 ,
,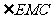 ,略
,略
(2)相等,略
生活拓展: 略
13.观察下列各图,寻找对顶角(不含平角):

 ⑴ 如图a,图中共有 对对顶角
⑴ 如图a,图中共有 对对顶角
⑵ 如图b,图中共有 对对顶角
⑶ 如图c,图中共有 对对顶角
⑷ 研究⑴-⑶小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,
则可形成 对对顶角
⑸ 若有2008条直线相交于一点,则可形成 对对顶角。
答案:轻松入门 1 对顶角 互为补角 2. 700 ,600,900 3.200 400 1200 1200
12. 如图∠AMB=90°,∠CMD=90°,ME、MF分别是射线MA、MD的反向延长线
⑴ 图中哪些角是∠EMF的余角?为什么?
⑵ ∠EMF与∠BMC是否相等?为什么?

生活拓展
11. 如图∠AOD=90°,OD为∠BOC的平分线,OE为BO的延长线,若∠AOB=40°,求∠COE的度数


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com