2.学生用量角器分别量一量各个角的度数,以发现各类角的度数有什么关系,学生得出有“相邻”关系的两角互补，“对顶”关系的两角相等.

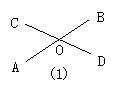
1.学生画直线AB、CD相交于点O,并说出图中4个角,两两相配共能组成几对角? 各对角的位置关系如何?根据不同的位置怎么将它们分类?

　　 学生思考并在小组内交流,全班交流.

　　 当学生直观地感知角有“相邻”、“对顶”关系时, 教师引导学生用几何语言准确地表达,如:

　　 ∠AOC和∠BOC有一条公共边OC,它们的另一边互为反向延长线.

　　 ∠AOC和∠BOD有公共的顶点O,而是∠AOC的两边分别是∠BOD两边的反向延长线.

　　 教师出示一块布片和一把剪刀,表演剪刀剪布过程,提出问题:剪布时,用力握紧把手,引发了什么变化?进而使什么也发生了变化?

　　 学生观察、思想、回答,得出:

　　 握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角边相应变小. 如果改变用力方向,随着两个把手之间的角逐渐变大,剪刀刃之间的角也相应变大.

　　 教师点评:如果把剪刀的构造看作两条相交的直线,以上就关系到两条相交直线所成的角的问题,本节课就是探讨两条相交线所成的角及其特征.

让同学们总结一下本节所复习的主要内容

6．如图所示，6枚硬币排成一个三角形，最少移动________枚硬币可以排成图(2)所示的环形。

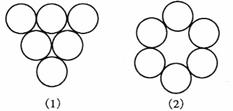
答：2

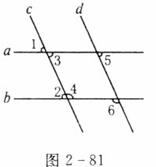
5．如图2-81

(1)如果a∥b，找出图中各角之间的等量关系。

(2)如果希望c∥d，那么需要哪两个角相等？

答：(1)a∥b，则图中各角之间的等量关系是：

∠1=∠2，∠1=∠3，∠3=∠2，∠1+∠4=180°，∠2+∠4=180°，∠3+∠4=180°∠5+∠6=180°。

(2)如果希望c∥d，那么需要∠3=∠5或者∠4=∠6。

4．如图2-80，在甲、乙两地之间要修一条笔直的公路，从甲地测得公路的走向是北

偏东42°，甲、乙两地同时开工，若干天后公路准确接通。乙地所修公路的走向是南偏西多少度?为什么?

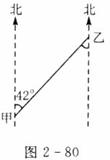
答：乙地所修公路的走向是南偏西42°。因为；两直线平行，内错角相等。

3．如图2-79所示，如果∠B与∠C互补，那么哪两条直线平行?∠A与哪个角互

补，可以保证AD∥BC?

答：如果∠B与∠C互补，那么线段AB与线段DC平行；∠A与∠B互补，可保证

AD∥BC。

理由都是：同旁内角互补，两直线平行。