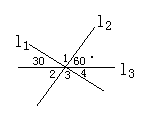
5.如图3所示,直线L₁,L₂,L₃相交于一点,则下列答案中,全对的一组是(　 )

　　　 A.∠1=90°,∠2=30°,∠3=∠4=60°;　　 B.∠1=∠3=90°,∠2=∠4=30

　　　 C.∠1=∠3=90°,∠2=∠4=60°;　　　　 D.∠1=∠3=90°,∠2=60°,∠4=30°

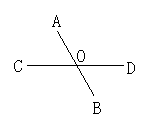
4.如图2所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为(　 )　　 A.62°　 　B.118°　　 C.72°　　 D.59°

3.下列说法正确的有(　 )

　　　 ①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.

　　　 A.1个　　 B.2个　　 C.3个　　 D.4个

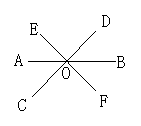
2.如图1所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于(　  )

A.150°　　 B.180°　　 C.210°　　 　D.120°

　　　　 (1)　　　　　　　　　 (2)　　　　　　　 (3)

1.如图所示,∠1和∠2是对顶角的图形有(　 )毛

　　　 A.1个　　 B.2个　　 C.3个　　 D.4个

2.练习:

课本P5练习.

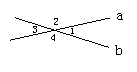
1.例:如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.

5.对顶角性质.

　　 (1)教师让学生说一说在学习对顶角概念后,结果实际操作获得直观体验发现了什么?并说明理由.

　　 (2)教师把说理过程,规范地板书:

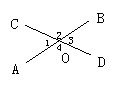
　　 在图1中,∠AOC的邻补角是∠BOC和∠AOD,所以∠AOC与∠BOC互补,∠AOC 与∠AOD互补,根据“同角的补角相等”,可以得出∠AOD=∠BOC,类似地有∠AOC=∠BOD.

　　 教师板书对顶角性质:对顶角相等.

　　 强调对顶角概念与对顶角性质不能混淆: 对顶角的概念是确定二角的位置关系,对顶角性质是确定为对顶角的两角的数量关系.

　　 (3)学生利用对顶角相等这条性质解释剪刀剪布过程中所看到的现象.

4.概括形成邻补角、对顶角概念.

　　 (1)师生共同定义邻补角、对顶角.

　　 有一条公共边,而且另一边互为反向延长线的两个角叫做邻补角.

　　 如果两个角有一个公共顶点, 而且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫对顶角.

　　 (2)初步应用.

　　 练习1:下列说法,你同意吗?如果错误,如何订正.

　　 ①邻补角的“邻”就是“相邻”，就是它们有一条“公共边”，“补”就是“互补”，就是这两角的另一条边共同一条直线上.

　　 ②邻补角可看成是平角被过它顶点的一条射线分成的两个角.

　　 ③邻补角是互补的两个角,互补的两个角也是邻补角?

3.学生根据观察和度量完成下表:

两直线相交	所形成的角	分类	位置关系	数量关系

　　 教师再提问:如果改变∠AOC的大小, 会改变它与其它角的位置关系和数量关系吗?