5.一个角的余角比它的补角的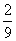还多1°，则这个的度数是＿＿

4.若∠α与∠β是对顶角，∠α=16°，则∠β=　　　 .　　　 　　　　　

两条直线相交所得的四个角中，有一个角是90°，

其余各角为 　　　　

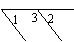
3.如图，∠1=∠2，则∠2与∠3的关系是　　　 ，　

∠1与∠3的关系是　　　 .

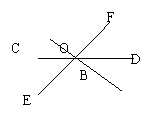
2.如图，三条直线AB.CD.EF相交于O点，

图中∠COF的对顶角是　　　　 .　　　　　　　　　　　　　　　　　　　　　　　　　　　　

1. 一个角的两边分别是另一个角的两边的_　 _______，这两个角叫对顶角．对顶角的性质是　　　　　　　　　　　 .

3．如图，直线EF与AB相交于G，与CD相交于H，则∠AGH的对顶角是___________;∠AGF与_______是对顶角.∠AGH与_______是邻补角,∠GHD的邻补角是________.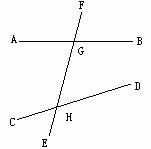

n　　　　 学法指导

引领激活　

活动:

拿出两根钉在一起的木条，张开一定角度生观察并回答下列问题：

　(l)用语言描述图形:直线a、b相交于点O.

　(2)这两条直线相交，构成了哪几个角．

　(3)模仿实物画一个图，用量角器测量各角度数．这四个角在数量上有什么关系？

范例点评　

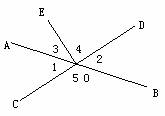[例1]　 如图，直线AB和CD直交于点O，OE是射线，则:

⑴∠1的对顶角是________,∠1的邻补角是______.

⑵∠5的对顶角是________,∠3的邻补角是______.

分析　 这道题是检查对顶角,邻补角的概念的,答题时应紧紧抓住这两个概念的本质特征来回答.

解 ⑴∠1的对顶角是∠2,∠1的邻补角是∠5和∠AOD.

⑵∠5的邻补角是∠AOD, ∠3的邻补角是∠BOE.

评注　 两条直线相交时,一个角的邻补角有两个,它们是对顶角,如例1中的∠1的邻补角,不能漏掉其中任何一个.

[例2] 如图,三条直线AB,CD,EF交于一点O,且OF平分∠DOB,试问:OE是不是∠AOC的平分线?为什么?

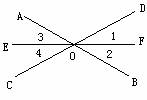
分析 判断OE是否为∠AOC的平分线,即考察∠3,∠4是否相等.由对顶角性质易知: ∠3=∠2, ∠4=∠1,而由条件可知∠1=∠2,所以可确定OE是∠AOC的平分线.

解　 OE是∠AOC的平分线.

理由如下:

因为　 OF平分∠DOB,

所以　 ∠1=∠2(角平分线定义)

因为　 ∠3=∠2　 ∠4=∠1(对顶角相等)

所以　 ∠3=∠4 (等量代换)

所以　 ∠OE是∠AOC的平分线. (角平分线的定义)

评注　 几何中某个结论成立的理由常用“因为 所以 ”的形式来表达．同学们应逐步熟悉和掌握．其中一步推理都要有根有据，在上面的解题过程中，我们把每一步的根据都写在后面的括号内，希望同学们开始也能这样做．

[例3] 如图，直线AB，CD，EF相交于点O，∠AOF=3∠FOB，∠AOC=90⁰，求∠EOC的度数．

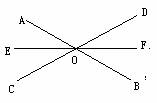
分析 由已知可知，∠EOC和∠AOE互余，所以求EOC的度数可先求∠AOE的度数，观察图形可知，∠AOE和∠BOF是对顶角，∠BOF和∠AOF是邻补角，利用它们的性质和已知条件，本题可解．

解　 设∠BOF=　x⁰,则∠AOF=3x⁰,

　 (邻补角定义)

解得x=45⁰,即∠BOF=45⁰

所以∠AOE=∠BOF=45⁰

所以∠EOC=∠AOC-∠AOE=45⁰

评注　 几何计算题，常用到几何图形中的性质，因此解也要有根有据，另外几何计算题也常得用代数方法达到解题目的．

n　　　　 师生互动

课堂交流

三条直线相交于一点,有多少对不同的对顶角?

四条直线相交于一点,有多少对不同的对顶角?

五条直线相交于一点,有多少对不同的对顶角?

n条直线相交于一点,有多少对不同的对顶角?

误区警示

判断两个角是否为对顶角，应注意满足以下三条件：⑴两条直线相交而成；⑵有一个公共点，⑶没有公共边．如图，∠1、∠2均不是对顶角．

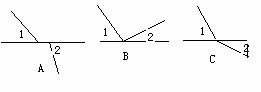
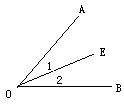“对顶角相等”这句话，反过说却不一定正确．如图，OE平分∠AOB，即∠1=∠2，但∠1与∠2不是对顶角．

检测评估

2.下列说法正确的是　 (　　 )．

A． 有公共顶点的两个角是对顶角．

B． 有公共顶点且相等的两上角是对顶角．

C． 两条直线相交所得的四个角中的任意两个角不是邻补角就是对顶角．

D． 相等的两个角一定是对顶角．

1.(2004江苏南京)如果∠α＝20°，那么∠α的补角等于(　　 )．

A. 20°　　　　 　　B. 70°　　　　　　 　C. 110°　　　　　 D. 160°

2、经历探索“对顶角相等”的性质，并会用它进行有关的简单推理和计算.

温故知新　

1、知道对顶角、邻补角的意义，能找出图形中一个角的对顶角和邻补角.