
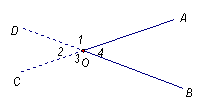
3.如图,直线AB、CD相交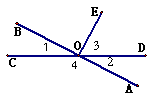 于O点,∠AOE=90°,
于O点,∠AOE=90°,
∠1和∠2是 角;
∠1和∠4互为 角;
∠2和∠3互为 角;
∠1和∠3互为 角;
∠2和∠4互为 角.
(2)通过两个例题的学习,体会对顶角相等、邻补角互补的应用。
例1
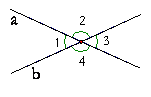 如图,直线a、b相
如图,直线a、b相
交,∠1=40°,求 ∠2、∠3、
∠ 4的度数.
变式1:若∠2是∠1的3倍,求∠3的度数。
变式2:若∠2比∠1大40度,求∠4的度数。
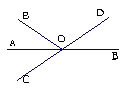
例2 如图,已知直线AB、CD相交于点O,
OA平分∠EOC,并且∠EOC=70°,求∠BOD的
度数.
例1的设置是要学生观察图形,应用知识,要求学生会表达,即:由什么,根据什么,得到什么。变式练习渗透用方程的思想解决几何问题的方法
例2的设置是结合前面的角平分线的知识与新知识组合,再次体会新知识的应用,培养学生思考问题的有序性
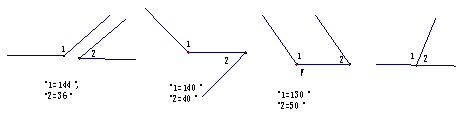
2.下列各图中,∠1和∠2是对顶角吗?为什么?
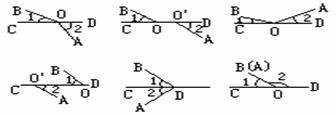
1.下列各图中∠1、∠2是邻补角吗?为什么?
5.3理解概念,巩固新知;
(1)通过3个识图题,巩固邻补角和对顶角的概念
5. 2逐步探究,形成新知:
2逐步探究,形成新知:
学生画出图形后,提出问题:
问题1:你能描述一下∠AOB与∠1有什么关系吗?你能给这对角起个新名字吗?
问题2:回忆刚才的作图,∠2是怎样形成的?∠2和∠4在位置上有什么特殊的关系吗?你能给∠4和∠2这对角起名吗?这两个角数量上有什么关系呢?
|
∵∠1与∠4互补,∠1与∠2互补 ∴∠4=∠2(同角的补角相等) |
即:对顶角相等
设计意图:让学生观察图形,抓住两个角的特点,尝试给出邻补角、对顶角的概念,培养学生数学语言的表达;进一步观察,得到对顶角相等的性质,训练学生由图形语言到文字语言,再到符号语言的三种语言的转换,培养学生几何语言的表达的能力,训练学生语言的表达的准确性;
5.1 回顾知识,感受必要
用几何画板演示学习几何知识简单的过程:点--直线、射线、线段--角,画出角的两边的延长线,引发新的知识--相交线。
意图是:回顾几何知识的学习过程,重温角的概念,利用已有的知识经验去探索,构想新概念,寻求新知识、新思路和新方法
6. 分层作业,获得进步。
下面就突出难点、突破难点作具体的说明:
5. 小结回顾,习惯反思;
4. 实际应用,体会必要;
3. 理解概念,巩固新知;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com