2.两条直线相交,如果它们所成的邻补角相等,那么一对对顶角就互补. (　 )

1.如果两个角有公共顶点和一条公共边,而且这两角互为补角, 那么它们互为邻补角. (　 )

2.选用课时作业设计.

课时作业设计

1.课本P9.1,2,P10.7,8.

2.练习:

　　 (1)课本P5练习.

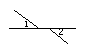
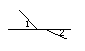
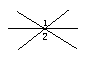
(2)补充:判断下列图中是否存在对顶角.

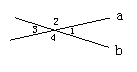
1.例:如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.

　　 教学时,教师先让学生辨让未知角与已知角的关系,用指出通过什么途径去求这些未知角的度数的,然后板书出规范的求解过程.

5.对顶角性质.

　　 (1)教师让学生说一说在学习对顶角概念后,结果实际操作获得直观体验发现了什么?并说明理由.

　　 (2)教师把说理过程,规范地板书:

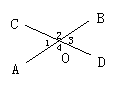
　　 在图1中,∠AOC的邻补角是∠BOC和∠AOD,所以∠AOC与∠BOC互补,∠AOC 与∠AOD互补,根据“同角的补角相等”,可以得出∠AOD=∠BOC,类似地有∠AOC=∠BOD.

　　 教师板书对顶角性质:对顶角相等.

　　 强调对顶角概念与对顶角性质不能混淆: 对顶角的概念是确定二角的位置关系,对顶角性质是确定为对顶角的两角的数量关系.

　　 (3)学生利用对顶角相等这条性质解释剪刀剪布过程中所看到的现象.

4.概括形成邻补角、对顶角概念.

　　 (1)师生共同定义邻补角、对顶角.

　　 有一条公共边,而且另一边互为反向延长线的两个角叫做邻补角.

　　 如果两个角有一个公共顶点, 而且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫对顶角.

　　 (2)初步应用.

　　 练习1:下列说法,你同意吗?如果错误,如何订正.

　　 ①邻补角的“邻”就是“相邻”，就是它们有一条“公共边”，“补”就是“互补”，就是这两角的另一条边共同一条直线上.

　　 ②邻补角可看成是平角被过它顶点的一条射线分成的两个角.

　　 ③邻补角是互补的两个角,互补的两个角也是邻补角?

3.学生根据观察和度量完成下表:

两直线相交	所形成的角	分类	位置关系	数量关系

　　 教师再提问:如果改变∠AOC的大小, 会改变它与其它角的位置关系和数量关系吗?

2.学生用量角器分别量一量各个角的度数,以发现各类角的度数有什么关系,学生得出有“相邻”关系的两角互补，“对顶”关系的两角相等.