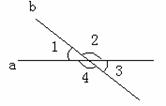
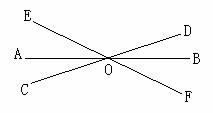
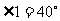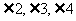例题：如图，直线a,b相交，，求的度数。

[巩固练习]

(教科书5页练习)

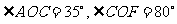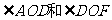已知，如图，，求：的度数

　[小结]

邻补角、对顶角.

　[作业]课本P9-1，2P10-7，8

　[备选题]

一判断题：

如果两个角有公共顶点和一条公共过，而且这两个角互为补角，那么它们互为邻补角(　 )

两条直线相交，如果它们所成的邻补角相等，那么一对对顶角就互补(　 )

二填空题

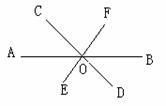
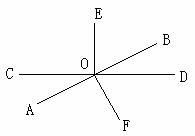
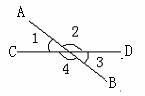
1如图，直线AB、CD、EF相交于点O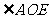，的对顶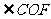角是　　　 ，的邻补角是　

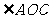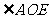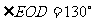若：=2：3，，则=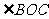　　

2如图，直线AB、CD相交于点O

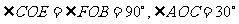则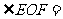　　

练习：

下列说法对不对

(1)　　　 邻补角可以看成是平角被过它顶点的一条射线分成的两个角

(2)　　　 邻补角是互补的两个角，互补的两个角是邻补角

(3)　　　 对顶角相等，相等的两个角是对顶角

学生利用对顶角相等的性质解释剪刀剪布过程中所看到的现象

4．概括形成邻补角、对顶角概念和对顶角的性质

2．学生用量角器分别量一量各角的度数，发现各类角的度数有什么关系？

(学生得出结论：相邻关系的两个角互补，对顶的两个角相等)

3学生根据观察和度量完成下表：

两条直线相交	所形成的角	分类	位置关系	数量关系

教师提问：如果改变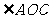的大小，会改变它与其它角的位置关系和数量关系吗

1．学生画直线AB、CD相交于点O，并说出图中4个角，两两相配共能组成几对角？根据不同的位置怎么将它们分类？

学生思考并在小组内交流，全班交流。

当学生直观地感知角有“相邻”、“对顶”关系时，教师引导学生用几何语言准确表达

；

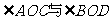有公共的顶点O，而且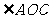的两边分别是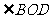两边的反向延长线

在我们的生活的世界中，蕴涵着大量的相交线和平行线，本章要研究相交线所成的角和它的特征。

观察剪刀剪布的过程，引入两条相交直线所成的角。

学生观察、思考、回答问题

教师出示一块布和一把剪刀，表演剪布过程，提出问题：剪布时，用力握紧把手，两个把手之间的的角发生了什么变化？剪刀张开的口又怎么变化？

教师点评：如果把剪刀的构造看作是两条相交的直线，以上就关系到两条直线相交所成的角的问题，

(七)布置作业

我布置了必做题和选做题，为学生提供个性化发展的空间，及时了解学生的学习效果，使学生养成独立思考，反思学习过程的习惯.

(六)、课堂小结

1、这节课学了哪些概念和性质？

2、你还有什么疑惑？

3、谈谈你对本节课的收获.

将本节课所学知识进行回顾和梳理，进一步培养他们归纳，总结能力.

(五)习题反馈

为了再次强化对顶角、邻补角的概念及对顶角性质的理解，我适当增加些练习，对于习题，循序渐进提高难度，让不同层次的学生都得于提高，对于趣味题和拓展题，学生通过思考，讨论，寻找规律，让他们进一步感觉“知识来源于实践”，同时学生的思路得于拓展.