1.下列各问题中的两个变量成反比例的是(　　 )；

A.某人的体重与年龄　　　　　　　 　　 B.时间不变时，工作量与工作效率

C.矩形的长一定时，它的周长与宽　　 　 D.被除数不变时，除数与商

3.已知y与x成反比例，并且当x = 2时，y = -1，则当x = -4时，y = 　　　.

2.有一面积为60的梯形，其上底长是下底长的 ，设下底长为x，高为y，则y与x的函数关系式是 　　　　　；

1.A、B两地相距120千米，一辆汽车从A地去B地，则其速度v(千米/时)与行驶时间t(小时)之间的函数关系可表示为 　　　　　；

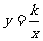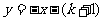2．如图，Rt_△ABO的顶点A是双曲线与直线在第二象限的交点，AB⊥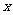轴于B且S_△ABO=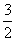

(1)求这两个函数的解析式

(2)求直线与双曲线的两个交点A，C的坐标和△AOC的面积。

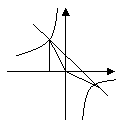
1．已知一次函数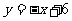和反比例函数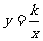(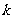≠0)

(1)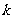满足什么条件时这两个函数在同一坐标系xoy中图象有两个公共交点。

(2)设(1)中的两个公共点为A，B，则∠AOB是锐角还是钝角。

(1)兄弟二人分吃一碗饺子，每人吃饺子的个数如下表：

①写出兄吃饺子数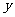与弟吃饺子数x之间的函数关系式(不要求写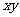的取值范围).

②虽然当弟吃的饺子个数增多时，兄吃的饺子数(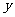)在减少，但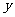与x是成反例吗？

(2)水池中有水若干吨，若单开一个出水口，水流速v与全池水放光所用时t如下表：

用时t(小时)	10	5		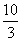	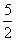2		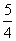1
	--……→逐渐减少
出水速度乙(吨/小时)	1	2	3	4	5	8	10
	--……→逐渐增大

①写出放光池中水用时t(小时)与放水速度v(吨/小时)之间的函数关系.

②这是一个反比例函数吗？

③与(1)的结论相比，可见并非反比例函数有可能“函数值随自变量增大而减小”，反之，所有的反比例函数都是“函数值随自变量的增大而减小吗？这个问题，你可以提前探索、尝试，也可以预习下一课时”反比例函数的图象和性质，也可以等到下一节课我们共同解决.

4．如果函数是反比例函数，那么k=________，此函数的解析式是____　 ____；

3．如果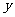与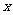成反比例，z与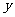成正比例，则z与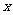成____　　　　 ______；

2．已知三角形的面积是定值S，则三角形的高h与底a的函数关系式是h =__________,这时h是a的__________；