2．某村有耕地346．2公顷，人数数量n每年发生变化，那么该村人均占有耕地面积m(公顷／人)是全村人口数n的函数吗？是反比例函数吗？为什么？

1．一个矩形的面积为20cm²，相邻的两条边长分别为xcm和ycm。那么变量y是变量x的函数吗？是反比例函数吗？为什么？

3．关键：从现实环境和所学知识人手，探索两个变量之间的相依关系。

教学过程：

问题提出：

电流I、电阻R、电压U之间满足关系式U=IR，当U=220V时，

(1)你所用含有R的代数式表示I吗？

(2)利用写出的关系式完成下表：

当R过来自大时，二怎样变化？当RN来越小呢？

(3)变量I是R的函数四？为什么？

数据提供的信息，并多用对关系式的分析，可以得出：当电阻R越来大时，电流I来越小，当R越来越小时，！越来越大。当给定一个R的值时，相应地就确定了一个I值，因此！是R的函数。

做一做。

2．难点：惯用反比例函数的概念．

1．重点：理解和领会反比例函数的概念。

2.经历抽象反比例函数概念的过程，领会反比例函数的意义，理解反比例函数的概念.

过程与方法目标：

　　 结合具体情境体会反比例函数的意义，能根据已知条件确定反比例函数表达式.

情感态度与价值观目标：

　　 结合实例引导学生了解所讨论的函数的表达形式，形成反比例函数概念的具体形象，是从感性认识到理性认识的转化过程，发展学生的思维；同时体验数学活动与人类生活的密切联系及对人类历史发展的作用.

重点、难点、关键：

1.从现实情境和已有的知识经验出发，讨论两个变量之间的相似关系，加深对函数概念的理解.

1．反比例函数

知识与技能目标：

　 备课资料

　　 参考例题

1.k为何值时，y=(k+2)x^k2-5是反比例函数

　　 分析：根据反比例函数表达式的一般形式y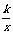＝ (k≠0)也可以写成y=kx^-1≠0),后一种写法中的x的次数为-1，可知此函数为反比例函数，必须具备两个条件：

　　 k+2≠0 k²-5＝-1

　　 二者缺一不可.

　　　 k+2≠0,　　　　 k≠-2,

解:由　　　　　　 得

k²-5=-1,　　　　 k=±2

　　 ∴k＝2.∴当k=2时，y=(k+2)x ^k2-5是反比例函数.

　　 常见错误：(1)不会把反比例函数的一般式y=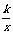写成y＝kx^-1的形式；

　　 (2)忽略了k+2≠0这个条件.

(1)菱形的面积一定时，菱形的两条对角线m和n属于反比例函数吗？为什么？

(2)计划修建铁路1200km，那么铺轨天数y是每日铺轨量x(km/d)的反比例函数吗？为什么？

(3)已知y+2与x-3成反比例，当x=1时，y=2；当x=2时，y=？

注：A等100-120分；B等90-99分；C等80-89分；D等70-79分；E等60-69分；F等0-59分