
1、把一张一百元的新版人民币把它换成50元的人民币,可得几张?换成10元的人民币可得几张?依次换成5元,2元,1元的人民币,各可得几张?换得的张数y 与面值x之间有怎样的关系呢?请同学们填表:
|
换成的元数x(元) |
50 |
20 |
10 |
5 |
2 |
1 |
|
换成的张数y(张) |
|
|
|
|
|
|
①用含有X的代数式表示Y?
②、当换成的元数X变化时,换成的张数Y会怎样变化呢?变量X是Y的函数吗?为什么?
第五章:反比例函数(第一课时)随堂资料
|
反比例函数 1、定义:一般地,如果两个变量x,y之间的关系可以表示成: 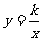 (k为常数,K≠0)的形式,那么称y是x的反比例函数。 (k为常数,K≠0)的形式,那么称y是x的反比例函数。2、注意: ①常数K≠0; ②自变量x不能为零(因为分母为0时,该式没意义); ③当 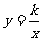 可写为 可写为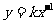 时注意x的指数为-1。 时注意x的指数为-1。④确定了k,这个函数就确定了。 |
自 由 空 间 (供作教学过程演练用) |
今天通过生活中的例子,探索学习了反比例函数的概念,我们要掌握反比例函数是针对两种变化量,并且这两个变化的量可以写成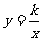 (k为常数,K≠0)同时要注意几点::①常数K≠0;②自变量x不能为零(因为分母为0时,该式没意义);③当
(k为常数,K≠0)同时要注意几点::①常数K≠0;②自变量x不能为零(因为分母为0时,该式没意义);③当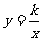 可写为
可写为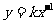 时注意x的指数为-1。④由定义不难看出,k可以从两个变量相对应的任意一对对应值的积来求得,只要k确定了,这个函数就确定了。
时注意x的指数为-1。④由定义不难看出,k可以从两个变量相对应的任意一对对应值的积来求得,只要k确定了,这个函数就确定了。
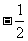
3、y是x的反比例函数,下表给出了x与y的一些值:
|
X |
|
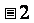 |
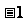 |
 |
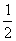 |
1 |
|
3 |
|
Y |
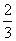 |
|
2 |
|
|
|
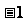 |
|
(1)写出这个反比例函数的表达式;(2)根据表达式完成上表。
教师巡视个别辅导,学生完毕教师给予评估肯定。
II巩固练习:限时(10分钟)完成附件:“随堂练习”5-13题。教师并给予指导、扭错。
2、某村有耕地346.2公顷,人口数量n逐年发生变化,那么该村人均占有耕地面积m(公顷/人)是全村人口数n的函数吗?是反比例函数吗?为什么?
I、学生完成资料的巩固练习1-4题:即
1、一个矩形的面积为20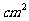 ,相邻的两条边长分别为Xcmt Ycm,那么变量Y是变量X的函数吗?是反比例函数吗?为什么?
,相邻的两条边长分别为Xcmt Ycm,那么变量Y是变量X的函数吗?是反比例函数吗?为什么?
(三)学生分组交流讨论
提示学生:数学来源于生活,请同学在生活中找出类似的例子。分组交流讨论,并完成资料的讨论部分。
我们再看例子: 两个变量x和y的乘积等于-6,用函数关系式表示出来是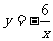 ,思考:变量x和y之间的关系是什么?
,思考:变量x和y之间的关系是什么?
提出问题:①变量之间的关系具有什么特点?引导学生得出:两个变量的乘积等于非零常数.②如何给反比例函数下定义?
教师总结并和学生一起探索出反比例函数的概念:
一般地,如果两个变量x,y之间的关系可以表示成: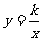 (k为常数,K≠0)的形式,那么称y是x的反比例函数。
(k为常数,K≠0)的形式,那么称y是x的反比例函数。
强调在理解概念时要注意:①常数K≠0;②自变量x不能为零(因为分母为0时,该式没意义);③当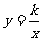 可写为
可写为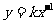 时注意x的指数为-1。④由定义不难看出,k可以从两个变量相对应的任意一对对应值的积来求得,只要k确定了,这个函数就确定了。
时注意x的指数为-1。④由定义不难看出,k可以从两个变量相对应的任意一对对应值的积来求得,只要k确定了,这个函数就确定了。
(二)互动探究,学习新课
我们知道,电流I、电阻R、电压U之间满足关系式U=IR,当U=220V时,(1)请你用含有R的代数式表示I;(2)利用你写出的关系式完成下表:
|
R/Ω |
20 |
40 |
60 |
80 |
100 |
|
I/A |
|
|
|
|
|
学生填表完成,提出当R越来越大时,I是怎样变化的?当R越来越小呢?(3)变量I是R的函数吗?为什么?
我们通过控制电阻的变化来实现舞台灯光的效果。在电压一定时,当R变大时,电流I变小,灯光就变暗,相反,当R变小时,电流I变大,灯光变亮。
引导学生看课本P131的例子,京沪高速公路全长约为1262km,汽车沿京沪高速公路从上海驶往北京,汽车完成全程所需的时间t(h)与行驶的平均速度V(km/h)之间有怎样的关系?变量t是v的函数吗?为什么?
(一)创设情境,引入新课
1、把一张一百元换成50元的人民币,可得几张?换成10元的人民币可得几张?依次换成5元,2元,1元的人民币,各可得几张?换得的张数y 与面值x之间有怎样的关系呢?请同学们填表:
|
换成的元数x(元) |
50 |
20 |
10 |
5 |
2 |
1 |
|
换成的张数y(张) |
|
|
|
|
|
|
提问:学生你会用含有X的代数式表示Y吗?并提出问题:当换成的元数X变化时,换成的张数Y会怎样变化呢?变量X是Y的函数吗?为什么?这就是我们今天要学生的反比例函数。我们再看课本的例子:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com