
1.两条直线被第三条直线所截,如果同位角相等,那么内错角也相等.( )
2.补充设计:
1.作业P18.1,2,3,4.
课本P17练习.
4.探索两条直线平行的其它方法
(1)演示教具,使学生直觉当内错角相等时,两条直线平行.
(2)让学生思考:为什么内错角相等时,两条直线平行?你能用学过的两直线平行的判定方法1来说明吗?
学生若有困难,教师可提示学生通过内错角和同位角之间的关系把条件∠2=∠3转化为∠1=∠2.
教师规范说理过程:因为∠2=∠3,而∠3=∠1(对顶角相等),所以∠1=∠2, 即同位角相等,因此a∥b.
(3)师生归纳判定两条直线平行的方法2,教师板书:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单记为:内错角相等,两直线平行.
教师引导学生结合图形用符号语言表达方法2:如果∠2=∠3,那么a∥b.
(4)讨论:同旁内角数量上满足什么关系时,两直线平行?
①学生猜想,可借助于教具.先排除相等,当∠4是锐角时,∠2是钝角才有可能使a∥b,进一步观察发现:如果同旁内角互补时,两条直线平行,即如果∠2+∠4=180 °,那么a∥b.
②学生利用平行判定方法1或方法2来说明猜想正确.
教师根据学生说理,再准确地板书:
因为∠4+∠2=180°,而∠4+∠1=180°,根据同角的补角相等,所以有∠2=∠1, 即同位角相等,从而a∥b.
因为∠4+∠2=180°,而∠4+∠3=180°,根据同角的补角相等,所以有∠3=∠2, 即内错角相等,从而a∥b.
③师生归纳两条直线平行的判定方法3,教师板书:
两条直线被第三条直线所截,如果同旁内角互补,那么两条直线平行.
简单记为:同旁内角互补,两直线平行.
综合图形,用符号语言表达:如果∠4+∠2=180°,那么a∥b.
3. 利用教具模型认识内错角和同旁内角.
利用教具模型认识内错角和同旁内角.
(1)教师展示教具模型,并在黑板上画出右图图型,指出在直线a、b被直线c所截成的角中,∠1和∠2是同位角,∠2与∠3、∠2与∠4虽然不是同位角, 但是它们又是具有某种位置关系的两个角,大家能叙述∠2与∠3有怎样的位置关系?∠2和∠4呢?
教师引导学生正确地叙述,如∠2与∠3位在直线a,b的内部,又分别位于直线c的两侧,∠2与∠4位在直线a,b内部,都在直线c的右侧(同侧).
(2)教师转动直线a或者直线b,再问学生∠2与∠3,∠2与∠4 的度数是否发生变化?它们之间的位置是否发生改变?
学生回答后,教师指出像∠2和∠3这样的两个角叫做内错角,像∠2和∠4这样的两个角叫做同旁内角.
(3)让学生识别图中其他的内错角和同旁内角,标记出它们.
(4)学生概括由直线a、b被直线c所截成的八个角中有四对的同位角, 两对的内错角、两对的同旁内角.
2.归纳利用同位角判定两条直线平行的方法.
(1) 学生根据同位角的意义以及平推三角尺画出平行线活动中叙述判定两条直线平行的方法.
教师引导学生正确表达平行线的判定方法1,并板书.
方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单记为:同位角相等,两条直线平行.
(2)教师引导学生,结合图形用符号语言表达两直线平行的判定方法1: 如果∠1=∠2,那么AB∥CD.
教师强调判定两直线平行方法1的条件中有两层意思:第一层这两个角是这两条被第三条直线所截而成的一对同位角;第二层这两个角相等两者缺一不可.
(3)简单应用.
①教师表演木工用每尺画平行线过程,让学生说出用角尺画平行线的道理(结合P15图5.2-7).
教师规范说理过程:因为∠DCB与∠FEB是直线CD、EF被AB所截而成的同位角,而且∠DCB=∠FEB,即同位角相等,根据直线平行判定方法,从而CD∥EF.
1.画出课本图5.2-5的简化图形,分析∠1、∠2的位置关系.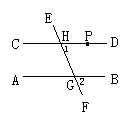
(1)让学生先描述∠1、∠2的方位.
(2)教师指出像∠1、∠2这样分别位于直线CD、AB的下方,又在直线EF的右侧, 也就是位置相同的两个角叫做同位角.
(3)让学生识别图中其他的同位角,并标记出它们,要求正确而又不遗漏.
(4)教师强调:同位角是具有特殊位置关系的两个角, 它不同于对顶角和邻补角.同位角都有一条边在截线EF上.
3.反思:在用直尺和三角形画平行线过程中,三角尺起着什么样的作用.
学生讲出是为画∠PHF,使所画的角与∠BGF相等.
教师指出既然两个角相等与两条直线平行能联系起来, 那么这两个角具有什么样的位置关系,我们是否得到了一个判定两直线平行的方法?这是本课要研究的内容之一.
2.画图:已知直线AB,点P在直线AB外,用直尺和三角尺画过点P的直线CD,使CD∥AB.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com