2.同一平面内,两条直线的位置关系

　　 教师引导学生从同一平面内,两条直线的交点情况去确定两条直线的位置关系.

　　 在同一平面内,两条直线只有两种位置关系:相交或平行,两者必居其一.即两条直线不相交就是平行,或者不平行就是相交.

1.结合演示的结论,师生用数学语言描述平行定义:同一平面内,存在一条直线a与直线b不相交的位置,这时直线a与b互相平行.换言之,同一平面内, 不相交的两条直线叫做平行线.

　　 直线a与b是平行线,记作“∥”,这里“∥”是平行符号.

　教师应强调平行线定义的本质属性,第一是同一平面内两条直线,第二是设有交点的两条直线.

3.教师组织学生交流并形成共识.

转动b时,直线b与c的交点从在直线a上A点向左边距离A点很远的点逐步接近A点,并垂合于A点,然后交点变为在A点的右边,逐步远离A点.继续转动下去,b与a 的交点就会从A点的左边又转动A点的左边……可以想象一定存在一个直线b的位置,它与直线a左右两旁都没有交点.

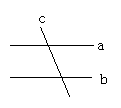
2.教师演示教具.

　　 顺时针转动木条b两圈,让学生思考:把a、b 想像成两端可以无限延伸的两条直线,顺时针转动b时,直线b与直线a的交点位置将发生什么变化?在这个过程中, 有没有直线b与c木相交的位置?

1.复习提问:两条直线相交有几个交点?相交的两条直线有什么特殊的位置关系?

　　 学生回答后,教师把教具中木条b与c重合在一起,转动木条a确认学生的回答.教师接着问:在平面内,两条直线除了相交外,还有别的位置关系吗?

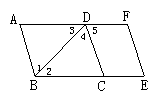
2.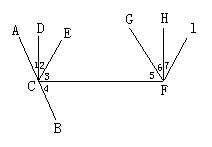右图,由图和已知条件,下列判断中正确的是(　 )

　 A.由∠1=∠6,得AB∥FG;　　　　　　　　　

B.由∠1+∠2=∠6+∠7,得CE∥EI

　 C.由∠1+∠2+∠3+∠5=180°,得CE∥FI;　　

D.由∠5=∠4,得AB∥FG

1.如图3所示,下列条件中,不能判定AB∥CD的是(　 )

　 A.AB∥EF,CD∥EF　　　　 B.∠5=∠A;　　 C.∠ABC+∠BCD=180°　　 D.∠2=∠3

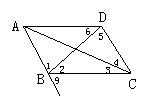
2.如图2,若∠2=∠6,则______∥_______,如果∠3+∠4+∠5+∠6=180°, 那么____∥_______,如果∠9=_____,那么AD∥BC;如果∠9=_____,那么AB∥CD.

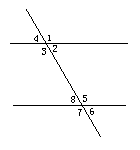
1.如图1,如果∠3=∠7,或______,那么______,理由是__________;如果∠5=∠3,或笔________,那么________, 理由是______________; 如果∠2+ ∠5= ______ 或者_______,那么a∥b,理由是__________.

　　　 (1)　　　　　　　　　　　 (2)　　　　　　　　　 (3)(

2.两条直线被第三条直线所截,如果内错角互补,那么同旁内角相等.(　 )