5.在同一平面内，两条不重合的直线的位置关系有　　　 种，是　　　 ．

4.在同一平面内，直线a与b满足下列条件，把它们的位置关系填在后面的括号内

⑴a与b没有公共点，则a与b　　　 ；

⑵a与b有且只有一个公共点，则a与b　　　　 ；

⑶a与b有两个公共点，则a与b　　　　　 ．

3. 互不重合的三条直线公共点的个数是 (　　 )．

　 　A.只可能是0个,1个或3个　B.只可能是0个,1个或2个

　 　C.只可能是0个,2个或3个　D.0个,1个,2个或3个都有可能

2. 在同一平面内，下列说法

⑴过两点有且只有一条直线

⑵两条不相同的直线有且只有一个公共点

⑶过一点有且只有一条直线与已知直线垂直

⑷过一点有且只有一条直线与已知直线垂直

其中正确的有(　　 )．

A　 1个 B 2个　 C 3个　　 D 4个

1.下列说法正确的是　 (　　 )．

A 两条不相交的直线叫做平行线

B 一条直线的平行线有且只有一条

C 若a∥b，a∥c，则b∥c．

D 两直线不相交就平行．

3.　　　 要注意区别垂线性质和平行公理在叙述上的不同，平行公理强调过直线外一点有且只有一条直线平行于已知直线，过直线上一点，不可以作已知直线的平行线．

检测评估

2.　　　 两条线段或射线不相交，不能确定，其一定平行，而是要看其所在直线是否相交．

1.　　　 空间范围内两条直线有三种不同的位置关系，相交、平行、异面．两条直线不相交，未必就平行，两直线平行，一定要在同一平面内．

3. 平行公理的内容是：_______________________________________.

学法指导

引领激活　

不相交就平行吗?

师：请同学们观察各人一个长方体实物，长方体的棱与棱不相交就平行吗？

学生：　　　　　　　　 ．

师：也就是说平行线的定义必须有怎样的前提条件？

学生：　　　　　　　　 ．

师：谁能说为什么要有这个前提条件？

学生：　　　 　　　　　　　．

范例点评　

[例1] 下列说法正确的是　 (　　 )．

A .同一平面内，两条直线的位置关系只有相交，平行两种.　

B .同一平面内，不相交的两条线段互相平行.

C .不相交的两条直线是平行线.

D .同一平面内，不相交的两条射线互相平行.　

分析 两条线段或两条射线平行是它们所在直线平行，两条射线或线段不相交不能保证它们所在直线不相交，故B，D错误；平行线不定是在同一平面内，若不在同一平面内，易找出既不相交，又不平行的直线，故C错误，根据平行线的定义易知A正确．

解　 选A

评注 在理解平行线概念要注意如下几点：⑴在同一平面内，如果两条直线不在同一平面内，即使不相交，也不一定平行．如图 (a)中的直线a,b.

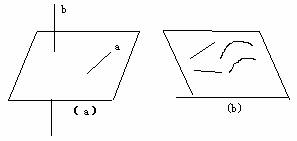
⑵是两条直线不相交，不是两条线段或射线也不是两条曲线，如图 B.中的线，它们虽然不相交，但却不是平行线．

⑶永不相交．两直线不相交，不仅是两直线画出的部分不相交，而是把它们无限制地画下去都不相交．

[例2] 对直线a,b若a∥b，c与a相交，那么c与b是什么关系？并说明理由．

分析　 由于已知条件中，没有交代a,b,c是否在同一平面内，故必须分下列两种情况讨论．⑴c在a和b所在的平面内；⑵c不在a和b所在平面内．

解 当c在a和b所在平面内时，若c∥b，由已知a∥b，根据平行公理的推论可得a∥c，这显然与已知条件c与a相交不符，所以c与b必相交．当c不在a和b所在的平面内，则c和b异面．

评注 当c在a和b所在平面内时，得到b和c相交，运用的是说明平行公理推论成立的方法．这种方法叫做反证法，今后我们还将进一步研究这一种方法．

n　　　　 师生互动

课堂交流

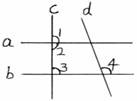
如图，下列哪些判断是不正确的：

(1)∵a⊥c，∴∠1=90°

(2)∵∠1=90°，∴∠2=90°

(3)∵a⊥c，b⊥c，∴a∥b

(4)∵∠3与∠4是同位角，∴∠3=∠4

误区警示

2. 在同一平面内,两条直线的位置关系只是__________.