
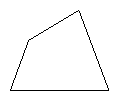
1.你能用一张不规则的纸(比如,如图1所示的四边形的纸)折出两条平行的直线吗?与同伴说说你的折法.
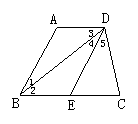
2.如图,直线AB、CD被直线EF所截,使∠1=∠2≠90°,则( )
A.∠2=∠4 B.∠1=∠4
C.∠2=∠3 D.∠3=∠4
1.如图,下列判断不正确的是( )
A.因为∠1=∠4,所以DE∥AB
B.因为∠2=∠3,所以AB∥EC
C.因为∠5=∠A,所以AB∥DE
 D.因为∠ADE+∠BED=180°,所以AD∥BE
D.因为∠ADE+∠BED=180°,所以AD∥BE
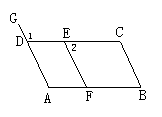
2. 如图,一个合格的变形管道ABCD需要AB边与CD边平行,若一个拐角∠ABC=72°,则另一个拐角∠BCD=_______时,这个管道符合要求.
如图,一个合格的变形管道ABCD需要AB边与CD边平行,若一个拐角∠ABC=72°,则另一个拐角∠BCD=_______时,这个管道符合要求.
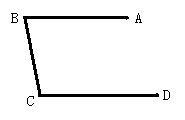
1.如图,点E在CD上,点F在BA上,G是AD延长线上一点.
(1)若∠A=∠1,则可判断_______∥_______,因为________.
(2)若∠1=∠_________,则可判断AG∥BC,因为_________.
(3)若∠2+∠________=180°,则可判断CD∥AB,因为____________.
(第1题) (第2题)
2.补充作业:
1.课本作业P19.5,6,8,9,10,12.
1.课本P18思考,教师要求学生说出尽可能多的判别方法和理由.
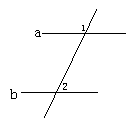 2.已知:如图,直线a、b被直线c所截,且∠1+∠2=180°,那么直线a与b平行吗? 为什么?
2.已知:如图,直线a、b被直线c所截,且∠1+∠2=180°,那么直线a与b平行吗? 为什么?
例:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
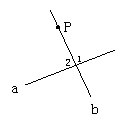
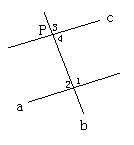
教师:这个问题的研究,就是回答了王玲折线方法的合理性.
首先王玲对折直线a,使折线过点P,于是把一个平角分成两个相等的∠1、∠2, 因为∠1+∠2=180°,所以∠1=∠2=90°.
其次王玲再对折折线b,使折线c过点P,很显然∠3=90°.
由垂直定义,可知a⊥b,c⊥b.
以上分析使学生明了垂直与直角总联系在一起.至于要判定两条直线是否平行,先考虑学过哪些判定平行线的方法,题中的条件与某种判定方法的条件是否相同?
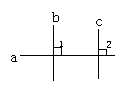 学生先口述判断与理由,教师纠正.并规范板书两步推理过程:
学生先口述判断与理由,教师纠正.并规范板书两步推理过程:
如课本P17图5.2-10.
因为b⊥a,c⊥a,
所以∠1=∠2=90°,
从而b∥c.
教师说明:这个道理过程有两个因为……所以…… . 第一个“因为”“所以”是根据垂直定义,第二个只写出“所以”的内容b∥c,中间省略一个“因为”的内容,这个内容就是第一个“所以”中的∠1=∠2.这样处理是使说理表达更简练, 第二个“因为”、“所以”是根据同位角相等,两直线平行.
例题讲解后,师提问:你还能利用其他方法说明b∥c吗?
教师鼓励学生模仿课本方法用图(1)内错角相等的方法写出理由,用图(2) 同旁内角互补的方法写出理由.
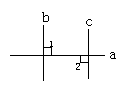
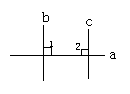
(1) (2)
 如果∠1,∠2不是同位角,也不是内错角、同旁内角,如图(3), 教师启发学生用化归思想将它转化为已知问题来解决,并且有条理地陈述理由:
如果∠1,∠2不是同位角,也不是内错角、同旁内角,如图(3), 教师启发学生用化归思想将它转化为已知问题来解决,并且有条理地陈述理由:
如图(3),
因为a⊥b,c⊥a,
所以∠1=90°,∠2=90°.
因为∠3=∠1=90°,
从而b∥c(同位角相等,两直线平行). (3)
3.教师再提出问题:你还有其他方法吗?动手试一试与同学们交流一下.
教师发现学生新的做法,组织学生交流,并归纳新的方法主要是:
(1)用尺规画过点P的与∠1相等的内错角∠3,达到作c∥a;
(2)再尺规画有别于李强的其他对同位角,达到作c∥a;
(3)用直尺、三角尺画出与王玲一样的线条,达到作c∥a.
在解释学生做法的合理性时,要求学生能利用“同位角相等,两直线平行”或“内错角相等,两直线平行”去说明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com