练习册

  • 练习册
  • 试题
     0  205308  205316  205322  205326  205332  205334  205338  205344  205346  205352  205358  205362  205364  205368  205374  205376  205382  205386  205388  205392  205394  205398  205400  205402  205403  205404  205406  205407  205408  205410  205412  205416  205418  205422  205424  205428  205434  205436  205442  205446  205448  205452  205458  205464  205466  205472  205476  205478  205484  205488  205494  205502  447090 

    5.2.2《直线平行的条件》教案

    教学内容
    		 直线平行的条件(第一课时)
    教学
    目标
    		 知识与技能
    		 了解同位角、内错角、同旁内角等角的特征，认识“直线平行”的三个充分条件及在实际生活中的应用。
    数学思考
    		 通过观察、思考探索等活动归纳出三种判定方法，培养学生转化的数学思想，培养学生动手、分析、解决实际问题的能力。
    解决问题
    		 通过活动及实际问题的研究引导学生从数学角度发现和提出问题，并用数学方法探索、研究和解决问题。
    情感态度
    		 感受数学与生活的紧密联系，体会数学的价值，激发学生学习数学的兴趣，培养敢想、敢说、敢解决实际问题的学习习惯。
    通过学生体验、猜想并证明，让学生体会数学充满着探索和创造，培养学生团结协作，勇于创新的精神。
    通过“转化”数学思想方法的运用，让学生认识事物之间是普遍联系，相互转化的辩证唯物主义思想。
    教　　 学
    重难点
    		 重　 点
    		 三种位置关系的角的特征； 会根据三种位置关系的角来判断两直线平等的方法。
    难　 点
    		 “转化”的数学思想的培养。
    由“说点儿理”到“用符号表示推理”的逐层加深。
    教学准备
    		 多媒体课件、直尺、三角板、塑料条
    教学方法
    		 指导探究法、类比法

    流程图
    		 活动内容和目的
    1、创设情景，引入新课
    		 通过活动，设置悬念，引入新课。
    2、实验操作，探索新知
    		 经历两条直线平行的方法探究，得出“同位角”与两直线平行的判定方法1。
    3、大胆猜想，探究新知
    		 类比同位角及判定方法1，猜想、证明两直线平行的判定方法2、3，及内错角与同旁内角。
    4、解释应用，巩固新知
    		 通过练习和应用所学知识，体会解决问题的方法。
    5、总结新知，布置作业
    		 回顾所学知识与方法，形成知识体系，应用、拓展、提高。

    教学流程　

    环节
    		 问题情境
    		 师生活动
    		 设计意图
    创设
    　情景
    　
    　
    　
    　
    孕育
    　新知
    		 观察图片、动画、回答问题：
    ①三幅图片从几何图形上看有什么共同点？
    ②比一比两张奖状粘贴的好坏，说一说，为什么？
    ③你见过木工师傅画平行线吗？
    		 教师展示图片和动画，提出问题。
    学生观察、思考、交流回答问题。了解实际生活中画平行线的广泛应用。
    		 通过图片和动画展示，贴近学生生活，激发学生的学习兴趣。从学生经历过的事入手。让学生知道数学知识无处不在，应用数学无时不有。
    符合“数学教学应从生活经验出发”的新课程标准要求
    实验
    操作
    　
    　
    　
    　
    　
    　探索
    新知
    		 1、如何过直线AB外一点P画直线AB的平行线CD？
    　
    　
    　
    　
    　
    　
    2、三角尺起什么作用？
    用学具摆两条平行线被第三条直线所截的模型。
    3、直线平行的条件1。
    4、练习：
    ①找出下图中的同位角，它们都相等吗？
    　
    　
    　
    　
    　
    ②你能说出木工师傅画平行线的依据吗？
    　
    　
    　
    　
    　
    ③∠1=30°，∠2=？ 时AB∥CD。
    　
    　
    　
    　
    		 1、教师展示动画，提出问题，学生探索时到学生中点拨。
    2、学生动手画平行线，操作学具摆两条平行线被第三条直线所截的模型，并探究角之间的位置关系，完成一组巩固练习。
    在这一环节中，教师应关注：①学生能否画平行线，动手操作是否准确
    ②学生能否独立探究、参与、合作、交流
    		 　
    复习提问，利用教具、学具让学生动手，提高学生学习兴趣，调动学生思考和积极性，提高学生合作交流的能力和质量，教师有的放矢，让学生掌握重点，培养学生自主探究的学习习惯和能力。
    及时练习巩固，，体现学以致用的观念，消除学生学无所用的思想顾虑。

    大胆
    猜想
    　
    　
    　
    　
    　
    　探究
    新知
    		 问题：
    ①∠2和∠3是什么位置关系？
    ∠3和∠4是什么位置关系？
    　
    　
    　
    　
    　
    　
    ②直线CD绕O旋转是否还保持上述位置关系？
    　
    　
    　
    　
    　
    　
    　
    ③∠2与∠3，∠2与∠4一定相等吗？
    问题：①∠2=∠3能得到AB∥CD吗？
    ②∠2+∠4=180可以判定AB∥CD吗？
    　
    　
    　
    　
    　
    练习：①由∠DCE= 　　　　　可以判定AD∥BE，由∠BAD+　　　　　　 =180° 可以判定AB∥CD
    　
    ②小明买了一幅画，你想知道上下边缘是否平行，你能帮他解决吗？
    		 教师提出问题，学生分组讨论，猜想，交流并发表意见。
    教师关注：①学生能否主动参与数学活动，敢于发表个人观点。
    ②小组团结协作程度，创新意识。
    ③表扬优秀小组
    　
    　
    　
    学习完成练习，落实新知。
    教师关注：
    ①学生能运用所学知识解决生活中的实际问题。
    ②学生语言表达说理的条理性。
    		 猜想、交流、归纳，符合知识的形成过程，培养学生转化的数学思想，学会将陌生的转化为熟悉的，将未知的转化为已知的。
    并用练习及时巩固，落实新知与方法，增强学生运用数学的能力。

    解释
    应用
    　
    　
    　
    　
    巩固
    新知
    		 问题：
    1、找出图中的同位角、同旁内角、内错角(口答)
    　
    　
    　
    　
    2、量得∠1=80°，∠2=　 　　　　　　可以判定AB∥CD，依据是　　　　　　　 ，由∠3=100° ，∠4=100° 可以判定　　　 ∥　　　 ，依据是 　　　　　　　。
    　
    　
    　
    　
    3、如图，因为∠ADE=∠DEF(已知)，所以　　　 ∥　　　 　。因为∠EFC+∠C=180°，所以EF∥　　　 　(　　　　 )，所以AD∥BC。
    　
    　
    　
    　
    　
    4、动手用相同的三角尺拼成如下图形，找出其中的平行线，说明理由。
    　
    　
    　
    　
    　
    5、P17练习
    		 教师提问，学生独立解答 。
    教师应关注：
    ①深入学生当中，对学习有困难学生进行鼓励，帮助。
    ②学生的思维角度是否合理。
    　
    		 加强学生运用新知的意识，培养学生解决实际问题的能力和学习数学的兴趣，让学生巩固所学内容，并进行自我评价，既面向全体学生，又照顾个别学有余力的学生，体现因材施教的原则。
    总结
    新知
    　
    　
    　
    　
    布置
    作业
    		 问题：
    通过本节学习，你认识哪几种位置关系的角？
    有哪几种判定直线平行的方法？
    遇到未知问题你会如何解决？
    　
    　
    布置作业：
    必做第18-19页，1、2、4题 。
    选做第19页，8题。
    		 教师设问，学生独立思考、回答、补充。
    教师关注：
    ①全体学生对本节知识的认识程度。
    ②学生是否愿意表达自己的观点。
    　
    		 通过提问方式引导学生进行小结，养成学习--总结--再学习的良好习惯，发挥自我评价作用，同时可培养学生的语言表达能力。
    作业分层要求，做到面向全体学生，给基础好的学生充分的空间，满足他们的求知欲。

    安排

    试题详情

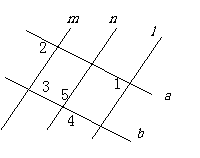
    4．如图，∠1=∠2，∠2=∠3，∠3+∠4=1800，找出图中互相平行的直线.

    　

    作业：教科书19页习题5.2第7、8题

    试题详情

    3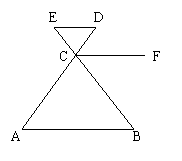．如图所示，已知∠D=∠A，∠B=∠FCB，试问ED与CF平行吗？

    试题详情

    2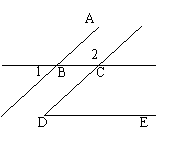．　如图所示，如果∠1=470，∠2=1330，∠D=470，那么BC与DE平行吗？AB与CD平行吗？

    试题详情

    1．教科书19页练习

    试题详情

    3．如图(2)

    (1)　　 如果∠1=∠D，那么______∥________；

    (2)　　 如果∠1=∠B，那么______∥________；

    (3)　　 如果∠A+∠B=1800，那么______∥________；

    (4)　　 如果∠A+∠D=1800，那么______∥________；

    新课：

    例1　 在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行吗？为什么？　

    分析：垂直总与直角联系在一起，我们学过哪些判断两条直线平行的方法？

    答：这两条直线平行.

    如图所示

    理由如下： ∵b⊥a,c⊥a

    ∴∠1=∠2=900(垂直定义)

    ∴b∥c(同位角相等，两直线平行)

    思考：

    　　 这是小明同学自己制作的英语抄写纸的一部分，其中的横格线互相平行吗？你有多少种判别方法？

    例2　　　　 如图所示，∠1=∠2，∠BAC=200，∠ACF=800.

    (1)求∠2的度数；

    (2)FC与AD平行吗？为什么？

    　　　　　　　　　　　　　　　

    巩固练习

    试题详情

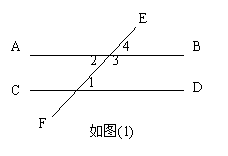
    2.如图(1)

    (1)如果∠1=∠4，根据_________________，可得AB∥CD；

    (2)如果∠1=∠2，根据_________________，可得AB∥CD；

    (3)如果∠1+∠3=1800，根据______________，可得AB∥CD .

    　

    试题详情

    复习提问：

    1．判定两条直线平行的方法有哪些？

    试题详情

    重点：判定两条直线平行方法的应用；

    难点：简单的逻辑推理过程.

    试题详情


    同步练习册答案