3、见下表：

根据上表写出y与x之间的关系式是：________________，y是否为x一的次函数？y是否为x有正比例函数？

2、下列函数关系中，哪些属于一次函数，其中哪些又属于正比例函数？

(1)面积为10cm²的三角形的底a(cm)与这边上的高h(cm)；

(2)长为8(cm)的平行四边形的周长L(cm)与宽b(cm)；

(3)食堂原有煤120吨，每天要用去5吨，x天后还剩下煤y吨；

(4)汽车每小时行40千米，行驶的路程s(千米)和时间t(小时)．

1、小明准备将平时的零用钱节约一些储存起来，他已有20元，从现在开始，每周存入5元，那么小明的存款y与从现在开始的周数x的关系为　　　　　　　　　　　　　 ．

2、能根据已知简单信息，写出一次函数的表达式.

补充练习：

5、巩固练习：书P149练习1,2

本课总结

4、例题讲解

例1：下列函数中，y是x的一次函数的是(　　 )

①y=x-6；②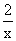y=；③y=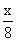；④y=7-x

A、①②③　 B、①③④　 C、①②③④　 D、②③④

例2：写出下列各题中x与y之间的关系式，并判断，y是否为x的一次函数？是否为正比例函数？

①汽车以60千米/时的速度匀速行驶，行驶路程中y(千米)与行驶时间x(时)之间的关系式；

②圆的面积y(厘米²)与它的半径x(厘米)之间的关系；

③一棵树现在高50厘米，每个月长高2厘米，x月后这棵树的高度为y(厘米)

例3：已知函数y=(m+1)x+(m²-1),当m取什么值时， y是x的一次函数？当m取什么值时，y是x的正比例函数？

例4、我国现行个人工资薪金税征收办法规定：月收入低于800元但低于1300元的部分征收5%的所得税……如某人某月收入11600元，他应缴个人工资薪金所得税为(1160-800)×5%=18(元)

①当月收入大于800元而又小于1300元时，写出应缴所得税y(元)与月收入x(元)之间的关系式.

②某人某月收入为960元，他应缴所得税多少元？

③如果某人本月缴所得税19.2元，那么此人本月工资薪金是多少元？

3、一次函数，正比例函数的概念

上面的两个函数关系式为y=0.5x+3，y=100-0.18x，都是左边是因变量y，右边是含自变量x的代数式.并且自变量和因变量的指数都是一次.

一般地，如果2个变量x与y之间的函数关系式，可以表示为y=kx+b(k，b为常数，且k≠0)的形式，那么称y是x的一次函数(x为自变量，y为因变量).

特别地，当b=0时，称y是x的正比例函数.

注意：1、自变量的指数为一次.2、含自变量的式子为整式.3、k ≠ 0

2、做一做

某辆汽车油箱中原有汽油100升，汽车每行驶50千米耗油9升.

(1)完成下表：

你能写出x与y之间的关系吗？

1、新课导入

有关函数问题在我们日常生活中随处可见，如弹簧秤有自然长度，在弹性限度内，随着所挂物体的重量的增加，弹簧的长度相应的会拉长，那么所挂物体的重量与弹簧的长度之间就存在某种关系，究竟是什么样的关系，请看：

某弹簧的自然长度为3厘米，在弹性限度内，所挂物体的质量x每增加1千克、弹簧长度y增加0.5厘米.

(1)计算所挂物体的质量分别为1千克、2千克、3千克、4千克、5千克时弹簧的长度，并填入下表：

(2)你能写出x与y之间的关系式吗？

分析：当不挂物体时，弹簧长度为3厘米，当挂1千克物体时，增加0.5厘米，总长度为3.5厘米，当增加1千克物体，即所挂物体为2千克时，弹簧又增加0.5厘米，总共增加1厘米，由此可见，所挂物体每增加1千克，弹簧就伸长0.5厘米，所挂物体为x千克，弹簧就伸长0.5x厘米，则弹簧总长为原长加伸长的长度，即 　　　　　　　　　　　　　　　　　　.

2、会根据已知信息写出一次函数的表达式.

教学过程：