(二)能力目标：

通过本节课的学习，培养学生的观察、分析和独立解决问题的能力。

(一)知识目标：

①根据图像和解析式探索并理解反比例函数的性质；

②逐步提高学生从函数图像中获得信息的能力，体会数形结合的思想方法。

1.　　　 教材的地位和作用：

函数是研究现实世界变化规律的重要数学模型。函数知识是初中代数的核心内容，随着学习的不断深入，函数把前面所学的方程、不等式等知识有机结合起来，成为解决代数知识的“桥梁”。学生在七年级下册“变量之间的关系”和八年级上册“一次函数”等内容中对函数有了初步了解，在此基础上讨论反比例函数图像与性质，可进一步领悟函数的概念，积累研究函数性质的方法以及用函数观点解决实际问题的经验，也为以后学习二次函数奠定基础。

2. 教学目标：

5、课堂小结

4、　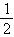 课堂练习：第129页1~3

3、反比例函数的性质

再让学生观察黑板上的图，提问：

　(1)当错误！不能识别的开关参数。 时，双曲线的两个分支各在哪个象限？在每个象限内，y随x的增大怎样变化？

(2)当错误！不能识别的开关参数。 时，双曲线的两个分支各在哪个象限？在每个象限内，y随x的增大怎样变化？这两个问题由学生讨论总结之后回答。

教师板书：

　(1)当k＞0时，函数图象的两个分支分别分布在第一、三象限内，在每一个象限中，y随x的增大而减小；当k＜0时，两个分支分别分布在第二、四象限内，在每一个象限中，y随x的增大而增大．

　(2)两个分支都无限接近但永远不能达到x轴和y轴．4、反比例函数的这一性质与正比例函数的性质有何异同？

例6、已知函数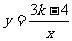在每一象限内，y随x的减小而减小，那么k的取值范围是　　

例7、在同一坐标系中，函数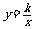和y=kx+3的图像大致是(　　　　　 )

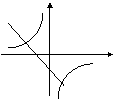
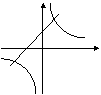
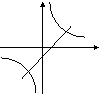
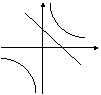
A　　　　　　　 B　　　　　　　　 C　　　　　　　　　　 D

2、反比例函数的图象

例6、画出反比例函数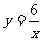与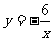的图象(师生分别画图)

步骤：(1)列表(强调x不能取0，为保证其图的对称性，x要取适当的值)

错误！不能识别的开关参数。

错误！不能识别的开关参数。

(2)描点(准确性要高)

(3)连线(用一条平滑曲线根据自变量由小到大的顺序把这些点连结起来)

归纳：

(1)反比例函数的图象由两条曲线组成，叫做双曲线。

(2)讨论反比例函数图象的画法：

①　　 反比例函数的图象不是直线，“两点法”是不能画的，它的图象是双曲线，图象关于原点成中心对称．列表时自变量的值可以选取绝对值相等而符号相反的数(如±1，±2等等)相应地就得到绝对值相等而符号相反的对应的函数值．这样即可以简化计算的手续，又便于在坐标平面内找到点．

②　　 反比例函数的图象的两支都无限地接近但永远不能达到x轴和y轴，所以图象与x轴y轴没有交点．如果发现画的图象“无限接近”坐标轴后，又偏离坐标轴，这也是错误的，教师可在课堂上演示，并说明错误的原因．

③　　 选取的点越多画的图越准确；

④　　 画图注意其美观性(对称性、延伸特征)

1、 反比例函数的定义

一般地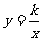，　 (k为常数，k≠0)叫做反比例函数，即y是x的反比例函数，也可以写成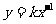

例3、　　　 知函数y=(m²+m-2)x^m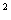-2m-9是反比例函数，求m的值。

例4、　　　 已知变量y与x成反比例，当x=3时，y=―6；那么当y=3时，x的值是　　 ；

例5、　　　 已知点A(―2，a)在函数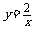的图像上，则a=　　 ；

议一议

想一想

(1)在一个反比例函数国家上任取两点P刀，过点P分别作X轴J轴的平行线，与坐标轴围成的矩形面积为SI；过点Q分别作x轴y轴的平行线，与坐标轴围成的矩形面积为有什么关系？为什么？

(2)将反比例函数的图像绕原点旋转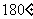后，能与原来的图像重合吗？

随堂练习：

课本随堂练习1、2。

课堂小结：

掌握反比例函数的主要性质．理解反比例函数的性质。

作业：

课本习题5．3　 1．2

2．例题教学

　　 例1先分析问题中的变量及变量间的关系，将用语言描述的函数关系表示为一次函数，然后根据函数值，求与之对应的自变量的值．

　　 例2是一道与“章头活动”相呼应、探索弹簧长度与力的大小关系的问题，是一次函数的一个物理模型．要求通过实验及记录的数据确定一次函数的解析式，求解过程示范了待定系数法的应用．