
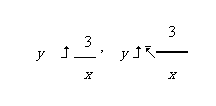
|
|
|
|
|
|
|
|

2、P149随堂练习
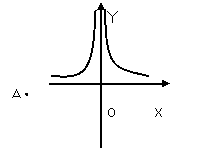
(二)、反比例函数的图象和性质
观察y=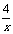 和y=
和y=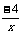 的图象的形状和位置,有什么相同点和不同点。(图象见课件)
的图象的形状和位置,有什么相同点和不同点。(图象见课件)
1、自己观察图象找出相同点和不同点。
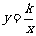
2、以同桌为一小组展开讨论反比例函数 的图象在哪两个象限,由什么确定。
3、引导总结。
结论:
形状:
图像分别都是由两支曲线组成,因此称反比例函数的图象为双曲线。
位置:
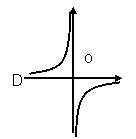
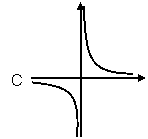
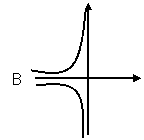
函数y=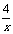 的两支曲线分别位于第一、三象限内.
的两支曲线分别位于第一、三象限内.
函数y=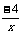 的 两支曲线分别位于第二、四象限内.
的 两支曲线分别位于第二、四象限内.
反比例函数的图象由k决定。
当k>0时,两支双曲线分别位于一,三象限内;
当k<0时,两支双曲线分别位于二,四象限内;
(一).画反比例函数的图象
1、复习根据函数解析式画函数图象的步骤。
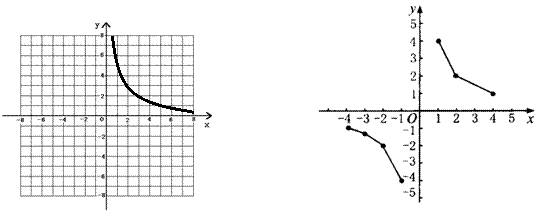
2、教师引导画出函数y=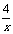 的图象。
的图象。
(1)列表:列表给出自变量与函数的一些对应值。(多媒体演示过程)
强调注意: ① x≠0
②列表时自变量取值易于计算,易于描点。
(2)描点.以表中对应值为坐标,在平面直角坐标系内描出相应的点. (多媒体演示过程)
连线.按照自变量由小到大的顺序,把所描的点用平滑的曲线连接起来. (多媒体演示过程)
(4)观察图象与一次函数的图象作对比.
3、出示下面四种不同类型的图象,学生找出正确的图象,并指出其他图象的错误。
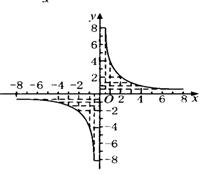
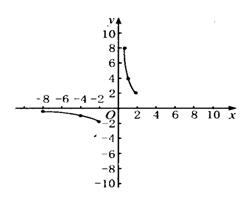
4、总结作反比例函数图象注意的问题。
(1).列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线 ,又可以使图象精确。
(2).描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错。
(3).一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接。
(4).图像是延伸的,注意不要画成有明确端点。
(5).曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交
5.做一做
请大家用同样的方法作反比例函数y=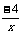 的图象.
的图象.
(1)、让学生自己作图。
(2)、多媒体出示正确的作图过程,让学生参考。
(3)学生修改自己的解题过程。
我们在前面学习了一次函数的图象,知道它们的图象都是一条直线,反比例函数y=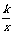 (k≠0)的图象是什么样子,这就需要我们动手去做一做,才能得出结论.本节课就让我们一齐来实践吧.
(k≠0)的图象是什么样子,这就需要我们动手去做一做,才能得出结论.本节课就让我们一齐来实践吧.
2.补充练习
1.随堂练习
4.想一想
3.做一做
2.议一议
相同点:
(1)图象都是由两支曲线组成:
(2)它们都不与坐标轴相交;
(3)它们都不过原点;
(4)它们都是轴对称图形,也是中心对称图形.
不同点:它们所在的象限不同,当k>0时,图象的两支曲线分别在第一、三象限内;当k<0时,图象的两支曲线分别位于第二、四象限.
Ⅴ.课后作业
习题5.2
Ⅵ.活动与探究
已知y=y1+y2,y1与x成正比例,y2与x2成反比例,且当x=2与x=3时,y的值都等于19.y与x间的系数关系式,并求x=4时y的值.
解:设y1=k1x,y2= .
∴y=y1+y2=k1x+
.
∴y=y1+y2=k1x+ .
.
当x=2时,y=19;
当x=3时,y=1.9.
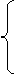 2k1+
2k1+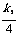 =19,
=19,
∴
3k1+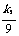 =19.
=19.
 k1=5.
k1=5.
解得
k2=36.
∴关系式为y=5x+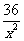 .
.
当x=4时,y=5×4+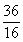 =20+
=20+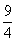 =22
=22
板书设计
§ 5.2.1 反比例函数的图象和性质(一)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com