
4. AB是⊙O直径,AB=4,F是OB中点,弦CD⊥AB于F,则CD=_________
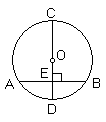
3. 如图,在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E.
则有AE=_____,
_____=  , ____=
, ____=  .
.
 1._____________________________________________________是轴对称图形.
1._____________________________________________________是轴对称图形.
2. 圆是_________________图形,其对称轴为_________________.
4.反比例函数的图象既不能与x轴相交也不能与y轴相交,但是当x的值越来越接近于0时,y的值将逐渐变得很大;反之,y的值将逐渐接近于0.因此,图象的两个分支无限接近;轴和y轴,但永远不会与x轴和y轴相交.
Ⅴ.课后作业
习题5.3
Ⅵ.活动与探究
反比例函数图象与三等分角
历史上,曾有人把三等分角问题归结为下面的作图问题.
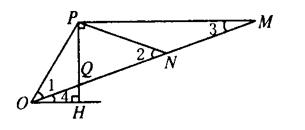
任取一锐角∠POH,过点P作OH的平行线,过点O作直线,两线相交于点M,OM交PH于点Q,并使QM=20P,设N为OM的中点.
∵NP=NM=OP,∴∠1=∠2=2∠3.
∵∠4=∠3,∴∠1=2∠4.
∴∠MOH=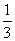 ∠POH.
∠POH.
问题在于,如何确定线段OM两端点的位置,并且保证O,Q,M在同一条直线上?事实上,用尺规作图无法解决这一问题.那么,退而求其次,能不能借助一些特殊曲线解决这一问题呢?
帕普斯(Pappus,公元300前后)给出的一种方法是:如下图,将给定的锐角∠AOB置于直角坐标系中,角的一边OA与y=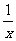 的图象交于点P,以P为圆心;以2OP为半径作弧交图象于点R.分别过点P和B作x轴和y轴的平行线,两线相交于点M,连接OM得到∠MOB.
的图象交于点P,以P为圆心;以2OP为半径作弧交图象于点R.分别过点P和B作x轴和y轴的平行线,两线相交于点M,连接OM得到∠MOB.
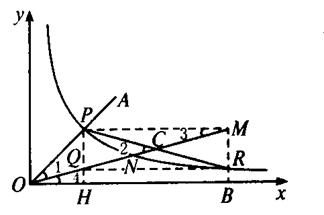
(1)为什么矩形PQRM的顶点Q在直线OM上?
(2)你能说明∠MOB=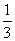 ∠AOB的理由吗?
∠AOB的理由吗?
(3)当给定的已知角是钝角或直角时,怎么办?
解:(1)设P、R两点的坐标分别为P(a1, ),R(a2,
),R(a2,  )则Q(a1,
)则Q(a1, ),M(a2,
),M(a2,  ).
).
设直线OM的关系式为y=kx.
∵当x=a2时,y=
∴ =ka2,∴k=
=ka2,∴k=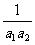 .∴y=
.∴y=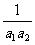 x.
x.
当x=a1时,y=
∴Q(a1, )在直线OM上.
)在直线OM上.
(2)∵四边形PQRM是矩形.
∴PC= PR=CM.∴∠2=2∠3.
PR=CM.∴∠2=2∠3.
∵PC=OP,∴∠1=∠2,
∵∠3=∠4,∴∠1=2∠4,
即∠MOB=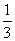 ∠AOB.
∠AOB.
(3)当给定的已知角是钝角或直角时,钝角或直角的一半是锐角,该锐角可以用此方法三等分.
3.将反比例函数的图象绕原点旋转180°后,能与原来的图形重合.即反比例函数是中心对称图形.
2.在一个反比例函数图象上任取两点P,Q,分别过P,Q作x轴、y轴的平行线,与坐标轴围成的矩形面积为S1,S2,则有S1=S2.
1.反比例函数y= 的图象,当k0时,在第一、三象限内,在每一象限内,y的值随,值的增大而减小;当k<O时,图象在第二、四象限内,y的值随x值的增大而增大.
的图象,当k0时,在第一、三象限内,在每一象限内,y的值随,值的增大而减小;当k<O时,图象在第二、四象限内,y的值随x值的增大而增大.
3.想一想
 (1)在一个反比例函数图象任取两点P、Q,过点Q分别作x轴,y轴的平行线,与坐标轴围成的矩形面积为S1;过点Q分别作x轴y轴的平行线,与坐标轴围成的矩形面积为S2,S1与S2有什么关系?为什么?
(1)在一个反比例函数图象任取两点P、Q,过点Q分别作x轴,y轴的平行线,与坐标轴围成的矩形面积为S1;过点Q分别作x轴y轴的平行线,与坐标轴围成的矩形面积为S2,S1与S2有什么关系?为什么?
(2)将反比例函数的图象绕原点旋转180°后.能与原来的图象重合吗?
[师]在下面的图象上进行探讨.
[生]设P(x1,y1),过P点分别作x轴,y轴的平行线,与
两坐标轴围成的矩形面积为S1,则S1=|x1|·|y1|=|x1y1|.
∵(x1,y1)在反比例函数y= 图象上,所以y1=
图象上,所以y1=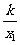 ,即x1y1=k.
,即x1y1=k.
 ∴S1=|k|.
∴S1=|k|.
同理可知S2=|k|,
所以S1=S2
[师]从上面的图中可以看出,P、Q两点在同一支曲线上,
如果P,Q分别在不同的曲线,情况又怎样呢?
[生]S1=|x1y1|=|k|,
S2=|x2y2|=|k|.
[师]因此只要是在同一个反比例函数图象上任取两点P、Q.不管P、Q是在同一支曲线上,还是在不同的曲线上.过P、Q分别作x.轴,y轴的平行线,与坐标轴围成的矩形面积为S1,S2,则有S1=S2.
(2)将反比例函数的图象绕原点旋转180°后,能与原来的图象重合,这个问题在上节课中我们已做过研究.
Ⅲ.课堂练习
P137
Ⅳ.课时小结
本节课学习了如下内容.
2.议一议
[师]刚才我们研究了y=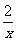 ,y=
,y=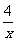 ,y=
,y= 的图象的性质,
的图象的性质,
下面用类推的方法来研究y=-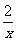 ,y=-
,y=-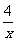 ,y=-
,y=- 的图象
的图象
有哪些共同特征?
[生](1)y=-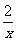 ,y=-
,y=-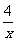 ,y=-
,y=- 中的k都小于0,它们的图象都位于第二,四象限,所以当A<0时,反比例函数的图象位于第二、四象限内.
中的k都小于0,它们的图象都位于第二,四象限,所以当A<0时,反比例函数的图象位于第二、四象限内.
(2)在图象y=-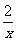 中,在第二象限内任取两点A(x1,y1),B(x2,y2),可知x1>x2,y1>y2,所以可以得出当自变量逐渐减小时,函数值也逐渐减小,即函数值y随自变量x的增大而增大.
中,在第二象限内任取两点A(x1,y1),B(x2,y2),可知x1>x2,y1>y2,所以可以得出当自变量逐渐减小时,函数值也逐渐减小,即函数值y随自变量x的增大而增大.
(3)这些反比例函数的图象不可能与x轴相交,也不可能与y轴相交.
[师]通过我们刚才的讨论,可以得出如下结论:
反比例函数y= 的图象,当k>0时,在每一象限内,y的值随x值的增大而减小;当k<0时,在每一象限内,y的值随x值的增大而增大.
的图象,当k>0时,在每一象限内,y的值随x值的增大而减小;当k<0时,在每一象限内,y的值随x值的增大而增大.
让学生积极投身于数学学习活动中,有助于培养他们的好奇心与求知欲.经过自己的努力得出的结论,不仅使他们记忆犹新,还能建立自信心.由学生自己思考再经过合作交流完成的数学活动,不仅能使学生学到知识,还能使他们互相增进友谊.
教学重点:通过观察图象,概括反比例函数图象的共同特征,探索反比例函数的主要性质.
教学难点:从反比例函数的图象中归纳总结反比例函数的主要性质.
教学方法:教师引导学生类推归纳概括学习法.
教具准备:多媒体课件
教学过程:
Ⅰ.创设问题情境,引入新课
[师]上节课我们学习了画反比例函数的图象,并通过图象总结出当k>0时,函数图象的两个分支分别位于第一、三象限内;当k<0时,函数图象的两个分支分别位于第二、四象限内.并讨论了反比例函数y=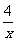 与y=-
与y=-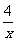 的图象的异同点.这是从函数的图象位于哪些象限来研究了反比例函数的.
的图象的异同点.这是从函数的图象位于哪些象限来研究了反比例函数的.
我们知道在学习正比例函数和一次函数图象时,还研究了当k>0时,y的值随x的增大而增大,当k<0时,y的值随x值的增大而减小,即函数值随自变量的变化而变化的情况,以及函数图象与x轴,y轴的交点坐标.本节课我们来研究一下反比例函数的有关性质.
Ⅱ. 新课讲解
1.做-做
 [师]观察反比例函数y=
[师]观察反比例函数y=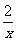 ,y=
,y=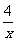 ,y=
,y= 的形式,它们有什么共同点?
的形式,它们有什么共同点?
[生]表达式中的k都是大于零的.
[师]大家的观察能力非同一般呐!
下面再用你们的慧眼观察它们的
图象,总结它们的共同特征.
 (1)函数图象分别位于哪几个象限?
(1)函数图象分别位于哪几个象限?
(2)在每一个象限内,随着x值的增大.y的值是怎样变化
的?能说明这是为什么吗?
(3)反比例函数的图象可能与x轴相交吗?可能与y轴相
交吗?为什么?
[师]请大家先独立思考,再互相交流得出结论.
[生](1)函数图象分别位于第一、三象限内.
(2)从图象的变化趋势来看,当自变量x逐渐增大时,
函数值y逐渐减小.
(3)因为图象在逐渐接近x轴,y轴,所以当自变量取很小或很大的数时,图象能与x轴y轴相交.
[师]大家同意他的观点吗?
[生]不同意(3)小的观点.
[师]能解释一下你的观点吗?
[生]从关系式y=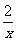 中看,因为x≠0,所以图象与y轴不可能能有交点;因为不论x取任何实数,2是常数,y=
中看,因为x≠0,所以图象与y轴不可能能有交点;因为不论x取任何实数,2是常数,y=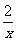 永远也不为0,所以图象与x轴心也不可能有交点.
永远也不为0,所以图象与x轴心也不可能有交点.
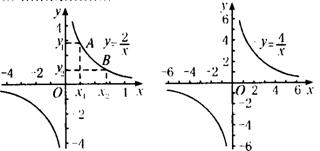
[师]对于(1)和(3)我不需要再说什么了,因为大家都回答的非常棒,不面我再补充-下(2).观察函数y=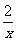 的图象,在第一象限我任取两点A(x1,y1),B(x2,y2),分别向x轴,y轴作垂线,找到对应的x1,x2,y1,y2,因为在坐标轴上能比较出x1与x2,y1与y2的大小,所以就可判断函数值的变化随自变址的变化是如何变化的.山图可知x1<x2,y2<y1,所以在第一象限内有y随x的增大而减小.
的图象,在第一象限我任取两点A(x1,y1),B(x2,y2),分别向x轴,y轴作垂线,找到对应的x1,x2,y1,y2,因为在坐标轴上能比较出x1与x2,y1与y2的大小,所以就可判断函数值的变化随自变址的变化是如何变化的.山图可知x1<x2,y2<y1,所以在第一象限内有y随x的增大而减小.
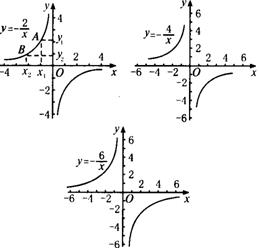 同理可知在其他象限内y随x的增大而如何变化.大家可以分组验证上图中的其他五种情况.
同理可知在其他象限内y随x的增大而如何变化.大家可以分组验证上图中的其他五种情况.
[生]情况都一样.
[师]能不能总结一下.
[生]当k>0时,函数图象分别位于第一、三象限
内,并且在每一个象限内,y随x的增大而减小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com