
1. 在半径为5的圆中,弦AB∥CD,AB=6,CD=8,试求AB和CD的距离.
3.还可以怎么说呢?能不能利用构造等腰三角形得出上面的等量关系?



 如右图示,连接OA、OB得到等腰△ABC,即OA=OB,因CD⊥AB,故△OAM与△OBM都是Rt△,又OM为公共边,所以两个直角三角形全等,则AM=BM,又⊙O关于直径CD对称,所以点A与点B关于CD对称,当圆沿着直径CD对折时,点A与点B重合,AC与BC重合AD与BD重合.因此AM=BM,AC=BC,AD =BD )
如右图示,连接OA、OB得到等腰△ABC,即OA=OB,因CD⊥AB,故△OAM与△OBM都是Rt△,又OM为公共边,所以两个直角三角形全等,则AM=BM,又⊙O关于直径CD对称,所以点A与点B关于CD对称,当圆沿着直径CD对折时,点A与点B重合,AC与BC重合AD与BD重合.因此AM=BM,AC=BC,AD =BD )
 4.在上述操作过程中,你会得出什么结论?
4.在上述操作过程中,你会得出什么结论?
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
[这就是利用圆的轴对称性得到的与圆相关的一个重要性质--垂径定理.在这里注意:①条件中的 “弦”可以是直径.②结论中的“平分弧”指平分弦所对的劣弧、优弦.
下面,我们一起看一下定理的证明:
如上图,连接OA、OB,则OA=OB
在Rt△OAM和Rt△OBM中,
∵ OA=OB,OM=OM
∴ Rt△OAM≌Rt△OBM
∴ AM=BM
∴ 点A和点B关于CD对称
∵ ⊙O关于直径CD对称



 ∴
当圆沿着直径CD对折时,点A和点B重合,AC和BC重合,AD 和BD重合
∴
当圆沿着直径CD对折时,点A和点B重合,AC和BC重合,AD 和BD重合



 ∴
AC=BC,AD =BD
∴
AC=BC,AD =BD
即垂径定理的条件有两项,结论有三项.用符号语言可表述为:
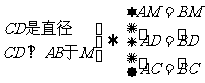
为了运用的方便,不易出现错误,易于记忆,可将原定理叙述为:一条直线若满足:(1)过圆心;(2)垂直于弦,那么可推出:①平分弦,②平分弦所对的优弧,③平分弦所对的劣弧.
例题讲解
通过求解例,来熟悉垂径定理以及常见的辅助线
已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.求证AC=BD.(证明略)

拓展延伸
2.很好.在上述的操作过程中,你发现了哪些相等的线段和相等的弧? 为什么呢?



 (AM=BM,AC=BC,AD =BD,因为折痕AM与BM互相重合,A点与B点重合.)
(AM=BM,AC=BC,AD =BD,因为折痕AM与BM互相重合,A点与B点重合.)
1.通过第一步,我们可以得到什么?
(可以知道:圆是轴对称图形,过圆心的直线是它的对称轴.)
4.将纸打开,新的折痕与圆交于另一点B,如上图.
教师叙述步骤,师生共同操作,并提出问题:
3.在⊙O上任取一点A,过点A作CD折痕的垂线,得到新的折痕,其中,点M是两条折痕的交点,即垂足.
2.得到一条折痕CD.
同学们想一想:圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
(圆是轴对称图形.过圆心的直线是它的对称轴,有无数条对称轴.)
你是用什么方法解决上述问题的?大家互相讨论一下.
我们可以利用折叠的方法,解决上述问题.把一个圆对折以后,圆的两半部分重合,折痕是一条过圆心的直线,由于过圆心可以作无数条直线。这样便可知圆有无数条对称轴.
圆是轴对称图形。过圆心的任意一条直线都是对称轴.
 做一做
做一做
按下面的步骤做一做:
1.在一张纸上任意画一个⊙O,沿圆周将圆剪下,把这个圆对折,使圆的两半部分重合.
6. ⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5
5. ⊙O直径为8,弦AB=4,则∠AOB=_____。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com