(二)、认识新知

　一个多面体总可以展开成一个平面图形，(多面体有几个面，它的平面展开图就是由几个面构成的)

　多面体具有的性质是：顶点数(V)+面数(F)－棱数(E)＝2(欧拉公式)

　例1、如图所示的图中，哪些能成为多面体的展开图？并指出多面体的名称。

例2、将一个正方体纸盒沿棱剪开成一个平面图形，有多少种不同的剪法？(排除经过平移、旋转、翻折可以重合的图形)解答：共有11种

(1)同一个正方体纸盒的表面沿不同的棱剪开，展开的平面图形是否相同？

(2)同一个正方体纸盒的表面沿不同的棱剪开，需要剪开多少个棱？(需要剪开7条棱，因六个面需5条棱连接)

(3)总结剪法：可通过选择①有四个正方形连在一排；②有三个正方形连在一排；③有二个正方形连在一排。

练习

1、下面每个图片都是6个大小相同的正方形组成的，其中不是正方体展开图的是(　)

2、下列平面图形中不是棱柱展开图的是(　　)

3、如图正方体的每一个面分别标有数字1、2、3、4、5、6，则可推出“？”处的数字是＿＿＿

解答：6

4、一个多面体的表面是由8个等边三角形组成的，当我们沿着它的棱把它剪开并展开为含8个等边三角形的平面图形，下列图形中有可能的是＿＿＿＿＿＿＿＿＿＿＿。

(一)、情境引入

　动手：(1)将一个长方体的纸盒展开成平面图形(可以有很多种展开方式)

　　(2)将一个圆柱体的侧面展开后是一个怎样的图形？

　　(3)将一个圆锥的侧面展是一个怎样的图形呢？

　准确判断简单多面体的平面展开图

目的与要求　认识立体图形与平面图形的关系，能根据展开图判断和制作简单的立体模型

知识与技能　多面体是由平面图形围成的立体图形，一个立体图形按不同的方式展开得到的平面图形可以是不一样的。

情感、态度与价值观　要熟练掌握简单多面体的平面展开图，可以从实例出发，多观察，多总结，在现实情境中去理解，积累操作经验。

2、长方体有　　　 个面，　　　 条棱，　　　 个顶点；五棱锥有　　　 个面，　　　 条棱，　　　 个顶点；若一个几何体的面数为f，棱数为e，顶点数为v，利用前面两个实例计算f + v – e =　　　　　 ，对于任意多面体上述结论都成立吗？

答：长方体有6个面，12条棱，8个顶点；五棱锥有6个面，10条棱，6个顶点；

f + v – e =2，对于多面体都存在上述结论(这就是著名的“欧拉公式”)。

[范例点睛]

如图3.3-6，下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色，那么涂黄色、白色、红色的对面分别是　　　　　　　　　　　　　　 (　　 )

A、蓝、绿、黑　　 B、绿、蓝、黑　　 C、绿、黑、蓝　　 D、蓝、黑、绿

答：选B。

思路点拨：从某一种颜色如白色可以确定与它相邻的颜色是黑、黄、绿、红，那么剩下的一种颜色蓝色就是它的对面颜色。

易错辨析：本题有可能不知道从什么地方入手，导致解题失败。

方法点评：抓住问题的关键--某一种颜色的相邻色，从而打开突破口。

[课外链接]

一只蜘蛛在一个正方体的顶点A处，一只蚊子在正方体的顶点B出，如图3.3-7所示，现在蜘蛛想尽快地捉到这只蚊子，那么它所走的最短路线是怎样的，在图上画出来，这样的最短路线有几条？

思路点拨：欲求从A到B的最短路线，在立体图形中难以解决，可以考虑把正方体展开成平面图形来考虑。如图3.2-8所示，我们都有这样的实际经验，在两点之间，走直路路程最短，因而沿着从A到B的虚线走路程最短。然后再把展开图折叠起来，在正方体上，象这样最短的路线一共有六条。

1、下列第二行的哪种几何体的表面能展开成第一行的平面图形？请对应连线。

答：连线如下图。

5.3　 展开与折叠(第二课时)

[新知导读]

5.4从三个方向看(1)

题目 5.4从三个方向看(1) 教学目标 经历从不同方向观察物体的活动过程，初步体会从不同方向看同一个物体所看到的形状往往是不同的，发展空间观念 能识别简单物体的三个视图 教学重点 识别简单物体的三个视图 教学难点 识别简单物体的三个视图 教学方法 引导发现式 教学工具 四棱柱，四棱锥，圆柱 教学内容 教师活动 学生活动

观察文具盒，分别从上看、从正面看、从侧面看，看到的结果是否相同？ 请分别画出从这三个方向看到的文具盒的草图 　 桌上放着一个长方体，一个锥体，和一个圆柱 说说下面三幅图分别是从哪个方向看到的 　　 　 举例说明日常生活中遇到上述的现象 从正面看到的图形称为主视图 从左面看到的图形称为左视图 从上面看到的图形称为俯视图 说明：一般将左视图画在主视图的右边，将俯视图画在主视图的下面 归纳总结三视图之间的关系： 主俯长相等，主左高平齐，俯左宽相等 　 画出所示物体的三个视图 1 　　　 　 2 　 物体有多少个小立方体？画出它的三视图 　 　　 练习 P100　 1，2 作业： P103 1，2，3 　 　 动手 　 　 　 　 　 　 　 　 　 　 　 动手 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 观察思考

2、下列图形是某些几何体的平面展开图，说出这些几何体的名称：

答：依次是：长方体、五棱锥、三棱柱。

[范例点睛]

如图3.3-2，某同学在制作正方体模型的时候，在方格纸上画出几个小正方形(图上阴影部分)，但是一不小心，少画了一个，请你给他补上一个，可以组合成正方体，你有几种画法，在图上用阴影注明。

答：画图如图3.3-3，有四种方法。

思路点拨：想象折叠成正方体时各个面所处的位置，看看缺哪个面，再确定在什么位置补画。

易错辨析：在想象困难时借助实物考虑。

方法点评：平面图形与立体图形之间的转换，在解题中应尽可能充分地想象，或借助实物。

[课外链接]

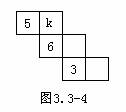
图3.3-4由六个正方形组成，将它们折叠可以组成一个正方体，正方体的表面编数码为1、2、3、4、5、6。有3个面上的数字漏写了，如果每一对面上的数的和都是7，求k的值。

思路点拨：想象一下折叠成的正方体，如果k处于上面的话，3正好与k相对处于底面。

　圆锥形纸筒、圆柱形纸筒和有盖和无盖的正方体盒子(以上师生人手一个)，粉笔盒、硬纸片，正方体的11种平面展开图。

[新知导读]

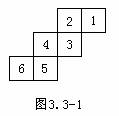
1、如图3.3-1在正方体的展开图上编号，请写出相对面(相对面没有公共棱)的号码：1对应(　　 )；2对应(　　 )；3对应(　　 )。

答：1对应4；2对应5；3对应6。