
|
平行线的性质 平行线具有的性质: 两条平行线的距离的概念 命题的概念 |
8.讨论
(1)“等式两边乘同一个数,结果仍是等式”是命题吗?它的题设和结论分别是什么?
(2)命题“两条平行线被第三条直线所截,内错角相等”是正确的吗?命题“如果两个角互补,那么它们是邻补角”呢?再举出一些命题的例子,讨论一下它们是否正确。
7.思考
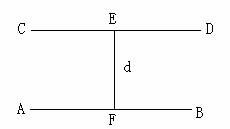
如下图,如果AB∥CD,在CD上任取一点E,向AB作垂线段EF,这时,EF是否也垂直于直线CD呢?我们这样作出的垂线段EF的长度d是平行线AB、CD的距离吗?
前面,我们学过一些对某一件事情作出判断的语句,例如:
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)等式两边加同一个数,结果仍是等式;
(3)对顶角相等。
像这样判断一件事情的语句,叫做命题(proposition)。许多命题都由题设和结论两部分组成。题设是已知事项,结论是由已知事项推出的事项。
命题通常写成“如果……那么……”的形式,这时,“如果”后接的部分是题设,“那么”后接的部分是结论。例如,上面的命题(1)中,“两条直线都与第三条直线平行”是题设,“这两条直线也互相平行”是结论。
6.探究
用三角尺和直尺画平行线,做成一张5× 5个格子的方格纸。观察做出的方格纸的一部分(图5.3-4),线段 BlC1, B2C2,…,B5C5都与两条平行的横线A1B5和A2C5垂直吗?它们的长度相等吗?

可以发现,线段BlC1, B2C2,…,B5C5同时垂直于两条平行的直线A1B5和A2C5,并且它们的长度相等。像这样,同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度,叫做这两条平行线的距离。
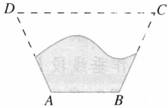
5.例 下图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形另外两个角分别是多少度?
[教法说明]学生在小学阶段对于梯形的两底平行就已熟知,所以学生能够想到利用平行线的同旁内角互补来找∠B和∠C的大小。这里学生能够自己解题,教师避免包办代替,可以培养学生积极主动的学习意识,学会思考问题,分析问题。学生板演教师指正,在几何里我们每一步结论的得出都要有理有据,规范学生的解题思路和格式,培养学生严谨的学习态度,修正学生的板演过程。
解:因为梯形上、下两底互相平行,所以∠A与∠D互补,∠B与∠C互补。于是
∠D=180°一∠A=180°一100°=80°,
∠C=180°一∠B=180°一115°=65°
所以梯形的另外两个角分别是80°、65°。
4.练习
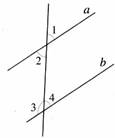
如图,直线a∥b,∠1=54°,那么∠2、∠3、∠4各是多少度?
3.思考
你能根据性质1,说出性质2、性质3成立的道理吗?例如:
如图5.3-2。
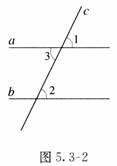
因为 a∥b,
所以 ∠l=∠2(_____)。
又∠3=______(对顶角相等),
所以∠2=∠3。
类似地,对于性质3,你能说出道理吗?
2.平行线具有性质:
性质1 两条平行线被第三条直线所截,同位角相等。
性质2 两条平行线被第三条直线所截,内错角相等。
性质3 两条平行线被第三条直线所截,同旁内角互补。
平行线的性质与判定
由角的关系得到两条直线平行的结论是平行线的判定,反过来,由已知直线平行,得到角相等或互补的结论是平行线的性质。
[教法说明]通过有形的具体实例,使学生在有充足的感性认识的基础上上升到理性认识,总结出平行线性质与判定的不同。
1.利用坐标纸上的直线或者用直尺和三角尺画两条平行线a∥b,然后,画一条截线c与这两条平行线相交,标出这些角(如下图)。
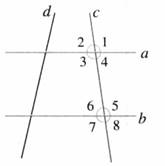
度量这些角,把结果填入下表:
|
角 |
∠1 |
∠2 |
∠3 |
∠4 |
|
度数 |
|
|
|
|
|
角 |
∠5 |
∠6 |
∠7 |
∠8 |
|
度数 |
|
|
|
|
各对同位角、内错角、同旁内角的度数之间有什么关系?写出你的猜想:
[教法说明]在教师提出问题的条件下,学生自己动手,实际操作,进行度量,在有了大量感性认识的基础上,动脑分析总结出结论,不仅充分发挥学生主体作用,而且培养了学生分析问题的能力。
两条平行线被第三条直线所截,同位角____,内错角____,同旁内角____。
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
学生活动:学生按老师的要求画出图形,并进行度量,回答出不论怎样画截线,所得的结论都一样。
思考:利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行。 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com