5.如图4, 已知: AP∥CQ, PB∥QD, ∠P＝80°则∠Q＝________°

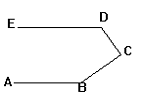
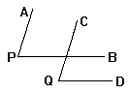
　　 图4　　　　　　　　　　　 图6

4.如图3：AB∥CD,∠A＝80°,∠B＝60°,则∠ACB＝____________度.

3.如图2：AB∥CD , A＝98°,∠C＝75°,∠B=_____度,∠D＝_____°.

2.如图1：当AD∥BC时,∠DAC＝∠________.

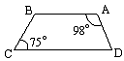
　 图1　　　　　　　　　　 图2　　　　　　　　　 图3

1.(2004江苏无锡)如图，已知a∥b，∠2=140°，则∠1=　　　　 °

3、思想目标：通过实际问题的深入和解决向学生渗透几何知识来源于实践并反作用于实践及认识事物的规律 是从特殊到一般，再从一般到特殊等辩证唯物主义观点．

温故知新　

(1)如图①，A.B.C三点在一条直线上．

如果∠3 =∠6，那么　　 ∥　　 ．(　　　　　　　　　　 )

如果∠6 =∠9，那么　　 ∥　　 ．(　　　　　　　　　　 )

如果∠1 +∠2 +∠3 =180°，那么　 ∥　 ．(　　　　 　　　　　　)

如果∠　 　=∠　　 ，那么BE∥CD．(　　　　　　　　　　 )

(2)如图②，看图填空：

∵∠1 =∠2(已知)

∴　　 ∥　　 ．(　　　　　　　　　　 )

又∵∠2 =∠3(已知)

∴　　 ∥　　 ．(　　　　　　　　　　 )

n　　　　 学法指导

引领激活　

在A.B两地之间要修一条公路(如图)．从A地测得公路的走向是北偏东60°．如果A.B两地同时开工，那么在B地公路按∠α=　　 度施工，能使公路准确接通．

范例点评　

[例1]　 如图 ，已知CD是∠ACB的平分线，DE∥BC，∠B=70⁰，∠ACB=50⁰，求∠ADE，∠DEC，∠EDC的度数．

分析 要求∠ADE，∠DEC，∠EDC的度数，主要是寻找这三个角与已知角的关系，由图形易知，∠ADE与∠B是同位角，∠DEC与∠ACB是同旁内角，而∠EDC与∠BCD是内错角．

解 ⑴∵DE∥BC

∴∠ADE=∠B　 (两直线平行，同位角相等)

∵∠B=70⁰

∴∠ADE=70⁰　 (等量代换)

⑵∵DE∥BC

∴∠DEC+∠ACB=180⁰(两直线平行，同旁内角互补)

∵∠ACB=50⁰

∴∠DEC=180⁰-50⁰=130⁰(等式性质)

⑶∵DE∥BC

∴∠EDC=∠BCD(两直线平行，内错角相等)

∵CD平分∠BCA

∴∠DCB=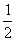∠BCA=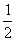×50⁰=25⁰

∴∠EDC=25⁰(等量代换)

[例2] 已知，如图 中，AC⊥AB，EF⊥BC，AD⊥BC，∠1=∠2，试问：AC⊥DG吗？请写出推理过程？

分析要考察AC与DG是否平行，为此只须判断∠1=∠3即可．

解 AC⊥DG

∵EF⊥BC，AD⊥BC(已知)

∴EF∥AD(垂直于同一直线的两直线平行)

∴∠2=∠3(两直线平行，同位角相等)

又∵∠1=∠2(已知)

∴∠3=∠1(等量代换)

∴DG∥AB(内错角相等，两直线平行)

∴∠BAC=∠DGC(两直线平行，同位角相等)

∵AB⊥AC(已知)

∴∠BAC=90⁰(垂直定义)

∴∠DGC=90⁰(等量代换)

∴DG⊥AC(垂直定义)

评注本例有一定的综合性，需有一定的分析问题的能力，几何中分析问题有两种基本方法：⑴由条件出发看能推出什么结论；⑵由要考察的问题看需满足什么条件，运用这两种方法，往能找到解决问题的思路．

[例3] 如图 ，AB∥EF，∠B=35⁰，∠F=42⁰，求∠BCF的度数．

分析∠BCF与∠B.∠F的关系并不明显，如果过C作一条直线平行于AB(EF)，那么∠BCF就被分成两个角，这两个角与∠B.∠F的关系就很清楚了．

解 经过点C画CD∥AB．

∴∠B=∠1 (两直线平行，内错角相等)

∵AB∥EF，CD∥AB

∴CD∥EF(平行于同一直线的两直线平行)

∴∠2=∠F(两直线平行，内错角相等)

∴∠BCF=∠1+∠2=∠B+∠F=35⁰+42⁰=87⁰．

评注在已知图形中本来没有CD这条平行线，是我们为了达到解题目的而添加的，在解题中起铺路架桥的作用，叫辅助线．

师生互动

课堂交流

(2004黄冈)

误区警示

平行线的性质和判定是两个不同的内容．由两角的关系得出两直线平行是平行线的判定，由两直线平行得出两角关系是平行线的性质，使用时不能混淆．

检测评估

2、智能目标：使学生领会数形结合、转化、对比的数学思想和方法，从而提高学生分析问题和解决问题的能力．

1、知识目标：使学生了解平行线的性质和判定的区别．掌握平行线的性质，并且会运用它们进行简单推理和计算．

5．3　　 平行线的性质

n　　　　 课前准备

学习目标　

3．如图，已知AD∥BC，可以得到哪些角的和为180°？已知AB∥CD，可以得到哪些角相等？并简述理由．