
2.补充作业:
1.课本P25.5,7,8,11,12.
2.第一个命题正确,第二个命题错误。可举出例子说明,如两条直线平行,同旁内角互补,但这两个同旁内角不是邻补角。对于学生所举的错误命题,教师应给归纳一下,有两类:第一类是命题题设不足于确定命题结正确,如“同位角相等”,这里条件不够;第二类命题是在命题的题设下,结论不正确。
2.命题“两条平行线被第三第直线所截,内错角相等”是正确的?命题“如果两个角互补,那么它们是邻补角”是正确吗?再举出一些命题的例子,判断它们是否正确.
解答:1.是命题,题设是“等式两边乘同一个数”,结论是“结果仍是等式”.
1.“等式两边乘同一个数,结果仍是等式”是命题吗?它们题设和结论分别是什么?
3.了解命题和它的构成.
(1)教师给出下列语句,学生分析语句的特点.
①如果两条直线都与第三条直线平行,那么这条直线也互相平行;
②等式两边都加同一个数,结果仍是等式;
③对顶角相等;
④如果两条直线不平行,那么同位角不相等.
这些语句都是对某一件事情作出“是”或“不是”的判断.
(2)给出命题的定义.
判断一件事情的语句,叫做命题.
教师指出上述四个语句都是命题,而语句“画AB∥CD”没有判断成分,不是命题.教师让学生举例说明是命题和不是命题的语句.
(3)命题的组成.
①命题由题设和结论两部分组成.题设是已知事项,结论是由已知事项推出的事项.
②命题的形成.
命题通常写成“如果……,那么……”的形式,“如果”后接的部分是题设,“那么”后接的部分是结论.
有的命题没有写成“如果……,那么……”的形式,题设与结论不明显,这时要分清命题判断了什么事情,有什么已知事项,再改写成“如果……,那么……”形式.
师生共同分析上述四个命题的题设和结论,重点分析第②、③语句.
第②命题中,“存在一个等式”而且“这等式两边加同一个数”是题设, “结果仍是等式”是结论。
第③命题中,“两个角是对顶角”是题设,“这两角相等”是结论。
2.实践与探究
(1)下列各图中,已知AB∥EF,点C任意选取(在AB、EF之间,又在BF的左侧).请测量各图中∠B、∠C、∠F的度数并填入表格.
|
∠B |
∠F |
∠C |
∠B与∠F度数之和 |
|
图(1) |
|
|
|
|
图(2) |
|
|
|
通过上述实践,试猜想∠B、∠F、∠C之间的关系,写出这种关系,试加以说明.
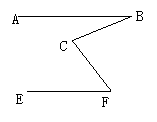
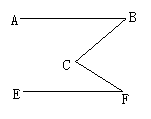
(1) (2)
教师投影题目:
学生依据题意,画出类似图(1)、图(2)的图形,测量并填表,并猜想:∠B+∠F=∠C.
在进行说理前,教师让学生思考:平行线的性质对解题有什么帮助? 教师视学生情况进一步引导:
①虽然AB∥EF,但是∠B与∠F不是同位角,也不是内错角或同旁内角. 不能确定它们之间关系.
②∠B与∠C是直线AB、CF被直线BC所截而成的内错角,但是AB与CF不平行.能不能创造条件,应用平行线性质,学生自然想到过点C作CD∥AB,这样就能用上平行线的性质,得到∠B=∠BCD.
③如果要说明∠F=∠FCD,只要说明CD与EF平行,你能做到这一点吗?
以上分析后,学生先推理说明, 师生交流,教师给出说理过程.
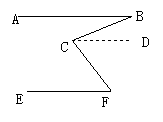
作CD∥AB,因为AB∥EF,CD∥AB,所以CD∥EF(两条直线都与第三条直线平行, 这两条直线也互相平行).
所以∠F=∠FCD(两直线平行,内错角相等).因为CD∥AB.
所以∠B=∠BCD(两直线平行,内错角相等).所以∠B+∠F=∠BCF.
(2)教师投影课本P23探究的图(图5.3-4)及文字.
①学生读题思考:线段B1C1,B2C2……B5C5都与两条平行线的横线A1B5和A2C5垂直吗?它们的长度相等吗?
②学生实践操作,得出结论:线段B1C1,B2C2……,B5C5同时垂直于两条平行直线A1B5和A2C5,并且它们的长度相等.
③师生给两条平行线的距离下定义.
学生分清线段B1C1的特征:第一点线段B1C1两端点分别在两条平行线上,即它是夹在这两条平行线间的线段,第二点线段B1C1同时垂直这两条平行线.
教师板书定义:
(像线段B1C1)同时垂直于两条平行线, 并且夹在这两条平行线间的线段的长度,叫做这两条平行线的距离.
④利用点到直线的距离来定义两条平行线的距离.
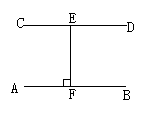
教师画AB∥CD,在CD上任取一点E,作EF⊥AB,垂足为F.
学生思考:EF是否垂直直线CD?垂线段EF的长度d是平行线AB、CD的距离吗?
这两个问题学生不难回答,教师归纳:
两条平行线间的距离可以理解为:两条平行线中,一条直线上任意一点到另一条直线的距离.
教师强调:两条平行线的距离处处相等,而不随垂线段的位置改变而改变.
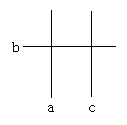
1.例1 已知:如上图,a∥c,a⊥b,直线b与c垂直吗?为什么?
学生容易判断出直线b与c垂直.鉴于这一点,教师应引导学生思考:
(1)要说明b⊥c,根据两条直线互相垂直的意义, 需要从它们所成的角中说明某个角是90°,是哪一个角?通过什么途径得来?
(2)已知a⊥b,这个“形”通过哪个“数”来说理,即哪个角是90°.
(3)上述两角应该有某种直接关系,如同位角关系、内错角关系、同旁内角关系,你能确定它们吗?
让学生写出说理过程,师生共同评价三种不同的说理.
4.a⊥b,c⊥b,那么a与c的位置关系如何?为什么?
3.完成下面填空.
已知:如图,BE是AB的延长线,AD∥BC,AB∥CD,若∠D=100°,则∠C=_____, ∠A=______,∠CBE=________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com