
4.学生验证猜测.
学生活动:再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
3.学生根据测量所得数据作出猜想.
图中哪些角是同位角?它们具有怎样的数量关系?
图中哪些角是内错角?它们具有怎样的数量关系?
图中哪些角是同旁内角?它们具有怎样的数量关系?
在详尽分析后,让学生写出猜想.
2.学生测量这些角的度数,把结果填入表内.
|
角 |
∠1 |
∠2 |
∠3 |
∠4 |
∠5 |
∠6 |
∠7 |
∠8 |
|
度数 |
|
|
|
|
|
|
|
|
1.学生画图活动:用直尺和三角尺画出两条平行线a∥b,再画一条截线c与直线a、b相交,标出所形成的八个角(如课本P21图5.3-1).
现在同学们已经掌握了利用同位角相等,或者内错角相等,或者同旁内角互补, 判定两条直线平行的三种方法.在这一节课里:大家把思维的指向反过来: 如果两条直线平行,那么同位角、内错角、同旁内角的数量关系又该如何表达?
|
5.3平行线的性质(1) 1.平行线的性质探究: 性质1: 例题: 练习: 性质2: 性质3: 2.平行线的性质与 判定的区别 |
(1)、教科书25页习题5.3第2、3、4题.
(2)、如图,AB∥CD,∠1=45°
∠D=∠C依次求出∠D、∠C、∠B的
度数.
[设计意图]:为学生提供个性化的发展的空间,及时了解学生的学习效果.
使学生养成独立思考、巩固、反思、提高学习过程的习惯.
(1)、通过这节课的学习活动,你有什么收获?你感受最深的是什么?
(2)、这节课得到的平行线的性质与平行线判定的方法有什么区别和联系?你能区分清楚吗?
学生自己先归纳后叙述.
[设计意图]:通过提出两个问题,让学生自己进行小结,回顾本节课所学的知识,并将本节课学的知识与前一节所学的知识进行比较、整理.有利于学生加以区分和为以后的应用打下基础.
[设计意图]:了解学生学习效果,让学生经历运用知识解决问题的过程,给学生以获得成功体验的空间,激发学习的积极性,建立学好数学的自信心.
5、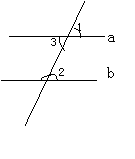 思考:你能用性质1,即“两条直线平行,同位角相等”说出性质2、性质3成立的道理吗?
思考:你能用性质1,即“两条直线平行,同位角相等”说出性质2、性质3成立的道理吗?
针对学生实际情况安排如下:
如图2,因为a∥b
所以∠1=∠2( )
又∠3= (对顶角相等)
所以∠2=∠3
类似地,对于性质3,你能说出道理吗?
多媒体演示,学生独立思考后完成填空.
[设计意图]:揭示三个性质之间的联系,加深学生对平行线性质的理解.同时也是循序渐进地引导学生思考,使学生初步养成言之有据的习惯,从而能逐步进行简单的推理.
|
|
|
||||
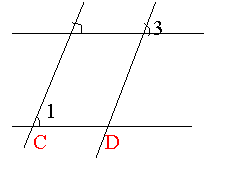
例2:如图,平行光线AB、DE照射在平面镜上,经反射得到
光线BC与EF,已知∠1= ∠2, ∠3= ∠4,则光线BC与EF
平行吗?为什么?

例题的教学步骤:
①、学生读题理解题意;②、学生独立思考,尝试解决;
③、教师适当分析;④、教师示范解题过程.
[设计意图]:本题有一定的逻辑性,学生先分组合作交流回答本组解法,然后我来以提问的方式来降低难度,本题的解题过程可作出示范,但一定要注意书写的规范,这个问题可帮助学生突破本节难点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com