3.两条平行线被第三条直线所截,则一对同旁内角的平分线互相平行.(　 )

2.两条直线被第三条直线所截,如果同旁内角互补,那么同位角相等.(　 )

1.两条直线被第三条直线所截,则同旁内角互补.(　 )

2.补充作业:

1.课本P25.1,2,3,4,6.

2.补充:如图,BCD是一条直线,∠A=75°,∠1=53°,∠2=75°,求∠B的度数.

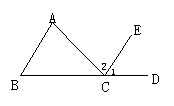
　　 本题综合应用平行线的判定和性质,教师要引导学生观察图形,考察已知角的数量关系,确定解题的思路.

1.课本练习(P22).

7.进一步研究平行线三条性质之间的关系.

　　 教师:大家能根据性质1,推出性质2成立的道理吗?

　　 结合上图,教师启发分析:考察性质1、性质2的结论发生了什么变化? 学生回答∠1换成∠3,教师再问∠1与∠3有什么关系?并完成说理过程,教师纠正学生错误,规范地给出说理过程.

　　 因为a∥b,所以∠1=∠2(两直线平行,同位角相等);

　　 又∠3=∠1(对顶角相等),所以∠2=∠3.

　 　教师说明:这是有两步的说理,第一步推理根据平行线性质1,第二步推理的条件不仅有∠1=∠2,还有∠3=∠1.∠2=∠3是根据等式性质.根据等式性质得到的结论可以不写理由.

　　 学生仿照以下说理,说出如何根据性质1得到性质3的道理.

　　 8.平行线性质应用.

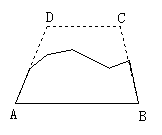
　　 例　 (课本P23)如图是一块梯形铁片的线全部分,量得∠A=100°,∠B=115°, 梯形另外两个角分别是多少度?

　　 教师把学生情况,可启发提问:①梯形这条件如何使用?②∠A与∠D、∠B 与∠C的位置关系如何,数量关系呢?为什么?

　　 讲解按课本.

6.教师引导学生理清平行线的性质与平行线判定的区别.

　　 学生交流后,师生归纳:两者的条件和结论正好相反:

　　 由角的数量关系(指同位角相等,内错角相等,同旁内角互补), 得出两条直线平行的论述是平行线的判定,这里角的关系是条件,两直线平行是结论.

　　 由已知的两条直线平行得出角的数量关系(指同位角相等,内错角相等, 同旁内角互补)的论述是平行线的性质,这里两直线平行是条件,角的关系是结论.

5.师生归纳平行线的性质,教师板书.

　　 平行线具有性质:

　　 性质1:两条平行线被第三条直线所截,同位角相等,简称为两直线平行, 同位角相等.

　　 性质2:两条平行线被第三条直线所截,内错角相等,简称为两直线平行, 内错相等.

　　 性质3:两条直线按被第三条线所截,同旁内角互补,简称为两直线平行, 同旁内角互补.

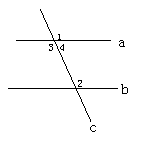
　　 教师让学生结合右图,用符号语言表达平行线的这三条性质,教师同时板书平行线的性质和平行线的判定.

　　 平行线的性质　　　　　　 平行线的判定

　　 因为a∥b,　　　　　　 因为∠1=∠2,

　　 所以∠1=∠2　　　　　 所以a∥b.

　　 因为a∥b,　　　　　　 因为∠2=∠3,

　　 所以∠2=∠3,　　　　　 所以a∥b.

　　 因为a∥b,　　　　　　 因为∠2+∠4=180°,

　　 所以∠2+∠4=180°,　　 所以a∥b.