
小结:
1.平行线的三个性质:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
活动4
解决问题.
问题1:如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=100°.请你求出另外两个角的度数.(梯形的两底是互相平行的)

学生活动设计:
学生思考后请学生回答,注意启发学生回答为什么,进一步细化为较为详细的推理,并书写出.
(解答)因为ABCD是梯形.
所以AD//BC.
所以∠A+∠B=180°,∠D+∠C=180°.
又∠A=115°,∠D=100°.
所以∠B=65°,∠C=80°.
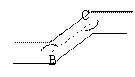
问题2:如图,一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角 B等于142°,第二次拐的角
B等于142°,第二次拐的角 C是多少度?为什么?
C是多少度?为什么?
学生活动设计:
学生根据拐弯前后的两条路互相平行容易得到∠B和∠C相等,于是得到∠C=142°
问题3:如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4.
(1)∠1、∠3的大小有什么关系?∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
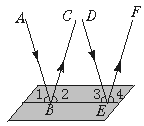
学生活动设计:从图中可以看出:∠1与∠3是同位角,因为AB与DE是平行的,所以∠1=∠3.又因为∠1=∠2,∠3=∠4,所以可得出∠2=∠4.又因为∠2与∠4是同位角,所以BC∥EF.
教师活动设计:这个问题是平行线的特征与直线平行的条件的综合应用.由两直线平行,得到角的关系用到的是平行线的特征;反过来,由角的关系得到两直线平行,用到的是直线平行的条件.同学们要弄清这两者的区别.
(解答)略.
问题4:如图,若AB//CD,你能确定∠B、∠D与∠BED的大小关系吗?说说你的看法.

学生活动设计:
由于有平行线,所以要用平行的知识,而∠B、∠D与∠DEB这三个角不是三类角中的任何一类,因此要考虑构造图形,若过点E作EF//AB,则由AB//CD得到EF//CD,于是图中出现三条平行线,同时出现了三类角,根据平行线的性质可以得到:∠B=∠BEF、∠D =∠DEF,因此∠B+∠D=∠BEF+∠DEF=∠DEB.
教师活动设计:
在学生探索的过程中,特别是构造图形这个环节,适当引导,让学生养成“缺什么补什么”的意识,培养学生的逻辑推理能力.
(解答)过点E作EF//AB.
所以∠B=∠BEF.
因为AB//CD.
所以EF//CD.
所以∠D=∠DEF.
所以∠B+∠D=∠BEF+∠DEF=∠DEB.
即∠B+∠D=∠DEB.
变式思考:
如图,AB//CD,探索∠B、∠D与∠BED的大小关系(∠B+∠D+∠DEB=360°).

试验1:教师以窗格为例,已知窗户的横格是平行的,用三角尺进行检验,发现同位角相等.这个结论是否具有一般性呢?
试验2:学生试验(发印制好的平行线纸单).
(1)要求学生任意画一条直线c与直线a、b相交;
(2)选一对同位角来度量,看看这对同位角是否相等.
学生归纳:两条平行线被第三条直线所截,同位角相等.
2.学生学法:在教师的指导下,积极思维,主动发现,认真研究.
教学模式:
探究发现教学模式.
教学方法:
直观教学法、发现教学法、主体互动法.
教学用具准备:
常用画图工具、量角器、白纸.
教学手段:
计算机辅助教学.
教学过程:
|
教学环节 |
教师活动 |
学生活动 |
教学意图 |
|
一 创 设 情 境 复 习 导 入 |
1.引入课题 如右图,世界著名的意大利比萨斜塔,建于公元1173年,为8层圆柱形建筑,全部用白色大理石砌成塔高54.5米. 目前,它与地面所成的较小的角为85º,它与地面所成的较大的角是多少度? 由此得出本节课题: 平行线的性质  2.复习回顾 平行线的判定方法有哪些? 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢? |
 观察、思考. 学生回答: 1.同位角相等,两直线平行. 2.内错角相等,两直线平行. 3.同旁内角互补,两直线平行. |
实际问题(存疑),创设情境,导入新课,既激发了学生学习新知识的积极性和主动性,又让学生感知到数学知识来源于实际生活,又服务于生活. 对上节课所学的判定方法进行复习回顾,并为新课的学习做准备. |
|
二 交 流 合 作 探 索 发 现  三 师 生 互 动 典 例 示 范 四 巩 固 知 识 拓 展 提 高 五. 梳理知 识 颗粒归 仓 |
合作交流一: 看课本第173页图4.8.9.(图略) 猜一猜∠1和∠2相等吗? 还有别的方法吗? 图中还有其它同位角吗?它们的大小有什么关系? 是不是任意一条直线去截平行线a、b所得的同位角都相等呢? [结论] 两条平行线被第三条直线所截,同位角相等. 简单说成:两直线平行,同位角相等. 符号语言:∵a∥b, ∴∠1=∠2. 合作交流二: 如图:已知a//b,那么Ð2与Ð 3相等吗?为什么? [结论]两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等. 符号语言:∵a∥b, ∴∠2=∠3. 合作交流三: 如图,已知a//b, 那么 Ð2与Ð4有什么关系呢? [结论]两条平行线被第三条直线所截,同旁内角互补. 简单说成:两直线平行,同旁内角互补. . 符号语言: ∵a∥b, ∴Ð 2+ Ð 4=180°. [大屏幕]例1如图,已知直线a∥b,∠1 = 500,求∠2的度数. 变式1.已知条件不变,求∠3,∠4的度数? 变式2.如图,已知∠3 =∠4, ∠1=47°, 求∠2的度数? 知识大冲浪 让学生进行选择: 1.超越号 如图在四边形ABCD中,已知AB∥CD, ∠B = 600. ①求∠C的度数; ②由已知条件能否求得∠A的度数? 2.创新号 如图,在汶川大地震当中,一辆抗震救灾汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么? 3.挑战号 小明在纸上画了一个角∠A,准备去测量它的度数,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC,FE的话,你能帮他设计出多少种方法测出∠A的度数? 最后回到引例. [总结]平行线的性质:由“线”定“角”, 平行线的判定:由“角”定“线”. |
猜一猜 量一量 拼一拼 想一想 看一看 由此得出平行线性质1.
学生回答 解∵a∥b(已知), ∴∠1=∠2(两直线平行, 同位角相等). ∵ ∠1=∠3(对顶角相等), ∴ ∠2=∠3(等量代换). 学生总结、表述 由此得出平行线性质2.
学生交流讨论并叙述. 解: ∵a//b (已知), ∴Ð 1= Ð 2(两直线平行, 同位角相等). ∵ Ð 1+ Ð 4=180° (邻补角定义), ∴Ð 2+ Ð 4=180° (等量代换). 学生总结、表述 由此得出平行线性质3.
积极思考 踊跃回答
猜测、讨论,寻找规律.
、
学生回答 学生畅谈收获 回顾、归纳. |
教师提出问题,引导学生分析,自己动手,实际操作,进行度量、观察,在有了大量感性认识的基础上,动脑分析总结出结论.不仅充分发挥学生主体作用,培养了学生观察分析问题的能力,还培养了学生的实践探究能力. 给学生留有充分的探索和交流的空间,鼓励学生利用多种方法探索,这对于发展学生的空间观念,理解平行线的性质是十分重要的. 学生从实践中得到的知识印象最深刻.在实验的基础上,组内同学相互帮助、争论、提示,能够进行推理证明. 锻炼学生的归纳、表达能力,鼓励学生敢于发表自己的观点. 培养学生的逻辑思维能力以及严谨的治学态度.逐步锻炼学生的推理能力,并进一步巩固对定理的理解及语言的规范,感受成功的喜悦,树立学习数学的信心. 要求学生会用平行线的性质进行简单的计算,只需算出所求的度数即可. 例1的变形目的是巩固平行线的三条性质. 通过教师指正,可以规范学生的解题思路和格式,培养学生严谨的学习态度. 可以培养学生积极主动的学习意识,学会思考问题,分析问题. 循序渐进提高难度,提高灵活运用定理的能力,感受解决有关平行问题的关键,突破难点,并进一步提高用符号语言进行推理的能力. 使学生的思路进一步得以拓宽,初次接触辅助线的添加,使学生能力得以提高. 学生情趣高涨. 将本节课知识进行回顾. |
||||||||||||||||||||||
|
六. 布置作业强化理 解 |
课本176页: 必做: 3,4,5 选做:B组 16 课后游戏:打一数学名词 1.齐头并进. 2.风筝跑了. |
课后完成. |
课后能进一步巩固,鼓励学生去发现身边的数学问题. |
1.教师教法:采用尝试指导、引导发现法,充分发挥学生的主体作用,体现民主意识和开放意识.
2.过程与方法目标:
(1)在与同学们的合作交流过程中,学会把实际问题转化为数学问题,获得解决问题的方法,拓宽思维能力.
(2)通过研讨与交流,在活动过程中学会与人合作,与人交流.
(3)学生通过活动感受知识的形成过程,加强对知识的理解.
1.知识与技能目标:
掌握平行线的三条性质, ,应用平行线的性质进行简单的推理和计算,培养学生观察分析能力和进行简单的逻辑推理能力.
2.(2002.哈尔滨)如图b所示,已知直线AB,CD被直线EF所截,若∠1=∠2,则∠AEF+∠CFE=________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com