2.课堂练习　 书：P159练习

总结：能利用一次函数及其图象解决简单的实际问题.

补充练习：

1)一根弹簧的原长为12 cm，它能挂的重量不能超过15 kg并且每挂重1kg就伸长cm写出挂重后的弹簧长度y(cm)与挂重x(kg)之间的函数关系式是　　　　　 (　 )

　　 A、y = x + 12(0＜x≤15　　　　　 B、y = x + 12(0≤x＜15

C、y = x + 12(0≤x≤15)　　　　 D、y = x + 12(0＜x＜15

2)如图公路上有A、B、C三站，一辆汽车在上午8时从离A站10千米的P地出发向C站匀速前进，15分钟后离A站20千米.

(1)　　　 设出发x小时后，汽车离A站y千米，写出y与x之间的函数关系式；

(2)　　　 当汽车行驶到离A站150千米的B站时，接到通知要在中午12点前赶到离B站30千米的C站.汽车若按原速能否按时到达？若能，是在几点几分到达；若不能，车速最少应提高到多少？

3)某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品，共50件.已知生产一件A种产品，需用甲种原料9千克、乙种原料3千克，可获利润700元；生产一件B种产品，需用甲种原料4千克、乙种原料10千克，可获利润1200元.

(1)、按要求安排A、B两种产品的生产件数，有哪几种方案？请你给设计出来；

(2)、设生产A、B两种产品获总利润为y (元)，其中一种的生产件数为x，试写出y与x之间的函数关系式，并利用函数的性质说明 (1)中哪种生产方案获总利润最大？最大利润是多少？

1.讲授新课

例题1、某居民小区按照分期付款的形式福利售房，政府给予一定的贴息.小明家购得一套现价为120000元的房子，购房时首期(第一年)付款30000元，从第二年起，以后每年应付房款为5000元与上一年剩余欠款利息的和，设剩余欠款年利率为0.4%.

1)若第x(x≥2)年小明家交付房款y元，求年付房款y(元)与x(年)的函数关系式；

2)将第三、第十年应付房款填入下表中：

例题2、已知雅美服装厂现有A种布料70米，B种布料52米，现计划用这两种布料生产M，N两种型号的时装共80套.已知做一套M型号的时装需要A种布料0.6米，B种布料0.9米，可获利润45元；做一套N型号的时装需要A种布料1.1米，B种布料0.4米，可获利润50元.若设生产N型号的时装套数为x，用这批布料生产这两种型号的时装所获总利润为y元.

(1)求y与x的函数关系式，并求出自变量的取值范围；

(2)雅美服装厂在生产这批服装中，当N型号的时装为多少套时，所获利润最大？最大利润是多少？

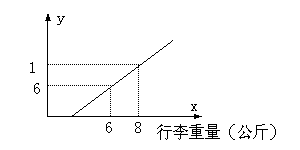
例题3、某地长途汽车客运公司规定，旅客可随身携带一定重量的行李，如果超过规定，则需要购买行李票，行李票费用y(元)是行李重量x(公斤)的一次函数，其图象如图所示.

求 (1)y与x之间的函数关系式

　 (2)旅客最多可免费携带行李的公斤数.

例题4、扬州火车货运站现有甲种货物1530吨，乙种货物1150吨，安排用一列货车将这批货物往广州，这列货车可挂A、B两种不同规格的货厢50节，已知用一节A型货厢的运费是0.5吨万元，用一节B型货厢的运费是0.8万元.

　 (1)设运输这批货物的总运费为y (万元)，用A型货的节数为x (节)，试写出y与x之间的函数关系式；

　(2) 已知甲种货物35吨和乙种货物15吨，可装满一节A型货厢，甲种货物25吨和乙种货物35吨吨可装满一节B型货厢，按此要求安排A、B两种货厢的节数，有哪几种运输方案？请你设计出来.

　(3)利用函数的性质说明，在这些方案中，哪种方案总运费最少？最少运费是多少万元？

3.通过函数来解决实际问题，使学生初步认识数学与人类生活的密切联系及对人类历史发展的作用，从而培养学生学习数学的兴趣，使他们能积极参与数学活动，进而更好地解决实际问题.

教学重点

一次函数的应用.

教学过程

2.通过解决实际问题，进一步发展学生的数学应用能力.

1.能利用一次函数及其图象解决简单的实际问题.

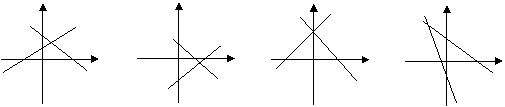
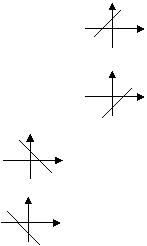
4.如图,两个一次函数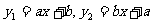,它们在同一直角坐标系中大致的图象是:

　　　　 y　　　　　　　　 y　　　　　　　 y 　　　　　　　　y

　　　　　　 y₁　　　　 y₁　　　　　　　　　 y₂

　　　 0　　　 x　　　　 0　　　 x　　　　 0　　　 x　　　　 0　 y₁ x

　　　　　　 y­₂ y₂　　　　　　　　　　　　 y₁　　 　　　y₂

　 　　　A.　　　　　　　 B.　　　　　　　 C.　　　　　　　 D

3、若一次函数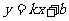的图象经过一、二、三象限,则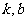应满足的条件是:

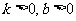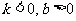A.　　 B.　　 C.　　 D.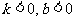

2、下列一次函数中，y的值随x值的增大而减小的是(　　 )

A.y=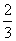x-8　 B.y=-x+3　 C.y=2x+5　 D.y=7x-6

1.下列一次函数中，y的值随x值的增大而增大的是(　　 )

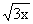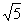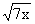A.y=-5x+3　 B.y=-x-7　 C.y=-　 D.y=-+4

3.一次函数y=kx+b的k、b的值对一次函数图象的影响.　　　　　　　　 y

①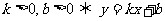的图象在一、二、三象限　　 0　 x

　　　　　　　　　　　　　　　　　　　　　　　　 　　　y

②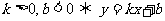的图象在一、三、四象限　 0　　 x

　　　　　　　　　　　　　　　　　　　　　　 y

③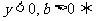图象在一、二、四象限　 0　　 x

　　　　　　　　　　　　　　　　　　　　　 y

④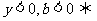图象在二、三、四象限　 0　　 x

　补充练习：