
3、如图5-9,正比例函数y=k1x的图象与反比例函数y=的图象相交于A、B两点,其中点A的坐标为(,2)
(1)分别写出这两个函数的表达式;
(2)你能求出点B的坐标吗?你是怎样求的?与同伴进行交流;
2、完成下表,并回答问题,如果以蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内?
|
R(Ω) |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
I(A) |
|
|
|
|
|
|
|
|
1、(1)蓄电池的电压为定值,使用此电源时,电流I(A)与电阻R(Ω)之间的函数关系如图5-8所示。
(2)蓄电池的电压是多少?你以写出这一函数的表达式吗?
电压U=36V , I=
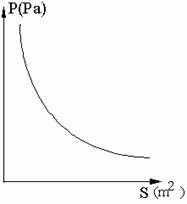
1、实例1:(1)用含S的代数式表示P,P是S的反比例函数吗?为什么?
答:P=(s>0),P是S的反比例函数。
(2)、当木板面积为0.2 m2时,压强是多少?
答:P=3000Pa
(3)、如果要求压强不超过6000Pa,木板的面积至少要多少?
答:至少0.lm2。
(4)、在直角坐标系中,作出相应的函数图象。
(5)、请利用图象(2)和(3)作出直观解释,并与同伴进行交流。
5.3 反比例函数的应用
|
课 题 |
5.3 反比例函数的应用 |
课型 |
新授课 |
|
|
教学目标 |
1.经历分析实际问题中变量之间的关系,建立反比例函数模型,进而解决问题的过程。 2.体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力。 |
|||
|
教学重点 |
掌握从实际问题中建构反比例函数模型。 |
|||
|
教学难点 |
从实际问题中寻找变量之间的关系。 |
|||
|
教学方法 |
自主探究法 |
|||
|
教学后记 |
|
|||
|
教 学 内 容 及 过 程 |
备注 |
|||
|
一、回顾交流、情境导入 某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地,为了安全、迅速通过这片湿地,他们沿着前进路线铺垫了若干块木板,构筑成一条临时通道,从而顺利完成了任务的情境。 问题思考: (1)请你解释他们这样做的道理。 (2)当人和木板对湿地的压力一定时,随着木板面积S(  )的变化,人和木板对地面的压强P(Pa)将如何变化? )的变化,人和木板对地面的压强P(Pa)将如何变化?(3)如果人和木板对湿地的压力合计600N,那么: ①用含S的代数式表示P,P是S的反比例函数吗?为什么? ②当木板面积为0.2  时,压强是多少? 时,压强是多少?③如果要求压强不超过6000Pa,木板面积至少要多大? ④在直角坐标系中,作出相应的函数图象。 ⑤请利用图象对(2)和(3)作出直观解释,并与同伴交流。 学生分四人小组进行探讨、交流。 二、寓思与练、小组探究 做一做 1.蓄电池的电压为定值,使用此电源时,电流I(A)与电阻R(  )之间的函数关系如图5-8所示: )之间的函数关系如图5-8所示:探究:(1)蓄电池的电压是多少?你能写出这一函数的表达式吗? (2)完成下表(课本P142),并回答问题,如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内? 学生独立思考,而后再进行全班交流,上讲台演示。 继续探究: 2.如图5-9,正比例函数  的图象与反比例函数 的图象与反比例函数 的图象相交于A、B两点,其中点A的坐标为( 的图象相交于A、B两点,其中点A的坐标为(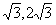 ) )探究:(1)请你分别写出这两个函数的表达式; (2)你能求出点B的坐标吗?你是怎样求的?与同伴交流。 学生独立思考,解答问题,上讲台演示自己的解答。 三、随堂练习 课本随堂练习 1 四、课堂总结 本节课是用函数的观点处理实际问题,关键在于分析实际情境,建立函数模型,并进一步明确数学问题,将实际问题置于已有的知识背景之中,用数学知识重新解释这是什么?可以看什么?逐步形成考察实际问题的能力,在解决问题时,应充分利用函数的图象,渗透数形结合的思想。 五、布置作业 课本习题5.4 1、2 |
|
|||
26.(1)0<k<9或k<0 (2)k<0时,∠AOB为钝角 0<k<9时,∠AOB为锐角
25.y=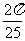 x2+
x2+
24.(1)y=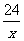 (2)略
(2)略
23.y=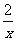
25.某厂要制造能装250mL(1mL=1 cm3)饮料的铝制圆柱形易拉罐,易拉罐的侧壁厚度和底部厚度都是0.02 cm,顶部厚度是底部厚度的3倍,这是为了防止“砰”的一声打开易拉罐时把整个顶盖撕下来,设一个底面半径是x cm的易拉罐用铝量是y cm3.
用铝量=底面积×底部厚度+顶部面积×顶部厚度+侧面积×侧壁厚度,求y与x间的函数关系式.
*26.已知直线y=-x+6和反比例函数y=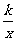 (k≠0)
(k≠0)
(1)k满足什么条件时,这两个函数在同一坐标系xOy中的图象有两个公共点?
(2)设(1)的两个公共点分别为A、B,∠AOB是锐角还是钝角?
单元测试
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com