1.经历分析实际问题中变量之间的关系，建立反比例函数模型，进而解决问题的过程.

　 备课资料

　　 参考练习

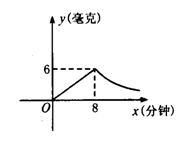
为了预防“非典”，

某学校对教室采用药熏

消毒，已知药物燃烧时，

室内每立方米空气中的

含药量y(毫克)与时

间x(分钟)成为正比例,药物燃烧后，y与x成反比例(如右图)，现测得药物8分钟燃毕，此时室内空气中每立方米的含药量6毫克，请根据题中所提供的信息，解答下列问题：

　　 (1)药物燃烧时，y关于x的函数关系式为　　　　 ,自变量x的取值范围为　　　　 ；

药物燃烧后，y关于x的函数关系式为　　　　 .

　　 (2)研究表明，当空气中每立方米的含药量低于1.6毫克时学生方可进教室，那么从消毒开始，至少需要经过______分钟后，学生才能回到教室；

　　 (3)研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效?为什么?

　　 答案：(1)y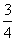＝x，　 0<x≤8　 y=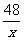

　　 (2)30

　　 (3)此次消毒有效，因把y=3分别代入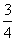y=x，y=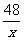，求得x＝4和x＝16，而16-4=12>10，即空气中的含药量不低于3毫克/m³的持续时间为12分钟，大于10分钟的有效消毒时间.

2.做一做(投影片§ 5.3 B，§ 5.3 C)

3．关键：充分运用所学知识分析实际情况，建立函数模型，教学中注意分析过程，渗透数形结合的思想。

教学过程：

某校科技小组进行野外考察，途中遇到一片十几米宽的烂泥湿地，

为了安全、迅速通过这片湿地，他们沿着前进路线铺垫了若干块木板，构筑成一条临时通道，从而顺利完成了任务。

问题思考：

(1)请你解释他们这样做的道理。

(2)当人和木板对湿地的压力一定时，M随着木板面积S(m²)的变化，人和木板对地面的压强P(Pa)将如何变化？

(3)如果人和木板对湿地的压力合计600N，那么：

①用含S的代数式表示PJ是S的反比例函数吗？为什么？

③当木板面积为0．2m²时，压强是多少？

③如果要求压强不超过6000Pa，木板面积至少要多大？

④在直角坐标系中，作出相应的函数国象。

随堂练习：

课本随堂练习1、2。

课堂小结：

本节课是用函数的观点处理实际问题，关键在于分析实际情境，建立函数模型，并进一步明确数学问题，将实际问题置于已有的知识背景之中，用数学知识重新解释这是什么？可以看什么？逐步形成考察实际问题的能力，在解决问题时，应充分利用函数的图像，渗透数形结合的思想．

作业：

课本习题5．4　 1．2

2．难点：从实际问题中寻找变量之间的关系。

1．重点：掌握从实际问题中建构反比例函数模型。

2.体会数学与现实生活的紧密联系，增强应用意识.提高运用代数方法解决问题的能力

过程与方法目标：

　　 通过对反比例函数的应用，培养学生解决问题的能力.

情感态度与价值观目标：

经历将一些实际问题抽象为数学问题的过程，初步学会从数学的角度提出问题。理解问题，并能综合运用所学的知识和技能解决问题.发展应用意识，初步认识数学与人类生活的密切联系及对人类历史发展的作用.重点、难点、关键：

1.经历分析实际问题中变量之间的关系，建立反比例函数模型，进而解决问题的过程.

3．反比例函数的应用

知识与技能目标：

P145~146　 1、2、3、4、5