
2.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,在这8个角中,有几对相等的角?请把它们分别表示出来:
___________________________________________________.
1.如图,△ABC的3个顶点都在⊙O上,∠ACB=40°,则∠AOB=_______,∠OAB=_____。
3.直径(或半圆)所对的圆周角是________,90°的圆周角所对的弦是_________。
2.在同圆或等圆中,同弧或等弧所对的圆周角_________,都等于该弧所对的圆心角的________.
1.顶点在_______,并且________都和圆相交的角叫做圆周角.
1.某蓄水池的排水管每时排水8 m3,6 h可将满池水全部排空.
(1)蓄水池的容积是多少?
(2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?
(3)写出t与Q之间的关系式;
(4)如果准备在5 h内将满池水排空,那么每时的排水量至少为多少?
(5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空?
解:(1)8×6=48(m3).
所以蓄水池的容积是48 m3.
(2)因为增加排水管,使每时的排水量达到Q(m3),所以将满池水排空所需的时间t(h)将减少.
(3)t与Q之间的关系式为 t=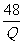 .
.
(4)如果准备在5 h内将满池水排空,那么每时的排水量至少为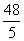 =9.6(m3).
=9.6(m3).
(5)已知排水管的最大排水量为每时12m3,那么最少要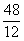 =4小时可将满池水全部排空.
=4小时可将满池水全部排空.
Ⅳ.课时小结
 节课我们学习了反比例函数的应用.具体步骤是:认真分析实际问题中变量之间的关系,建立反比例函数模型,进而用反比例函数的有关知识解决实际问题.
节课我们学习了反比例函数的应用.具体步骤是:认真分析实际问题中变量之间的关系,建立反比例函数模型,进而用反比例函数的有关知识解决实际问题.
Ⅴ课后作业
习题5.4.
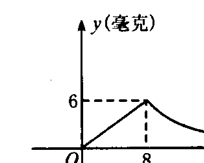
为了预防“非典”,
某学校对教室采用药熏消毒,已知药物燃烧时,
室内每立方米空气中的含药量y(毫克)与时
间x(分钟)成为正比例,药物燃烧后,y与x成反比例
(如右图),现测得药物8分钟燃毕,此时室内空气中
每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范围为 ;
药物燃烧后,y关于x的函数关系式为 .
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
答案:(1)y=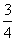 x, 0<x≤8 y=
x, 0<x≤8 y=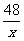
(2)30
(3)此次消毒有效,因把y=3分别代入y=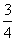 x,y=
x,y=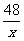 ,求得x=4和x=16,而16-4=12>10,即空气中的含药量不低于3毫克/m3的持续时间为12分钟,大于10分钟的有效消毒时间.
,求得x=4和x=16,而16-4=12>10,即空气中的含药量不低于3毫克/m3的持续时间为12分钟,大于10分钟的有效消毒时间.
2.如下图,正比例函数y=k1x的图象与反比例函数y=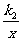 的图象相交于A,B两点,其中点A的坐标为(
的图象相交于A,B两点,其中点A的坐标为(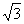 ,2
,2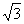 ).
).
(1)分别写出这两个函数的表达式:
(2)你能求出点B的坐标吗?你是怎样求的?与同伴进行交流.
[师]要求这两个函数的表达式,只要把A点的坐标代入即可求出k1,k2,求点B的
坐标即求y=k1x与y=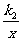 的交点.
的交点.
[生]解:(1)∵A(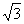 ,2
,2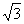 )既在y=k1x图象上,又在y=
)既在y=k1x图象上,又在y=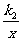 的图象上.
的图象上.
∴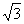 k1=2
k1=2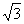 ,2
,2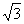 =
=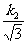 .
.
∴k1=2, k2=6
∴表达式分别为y=2x,y=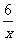 .
.
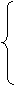 y=2x,
y=2x,
(2)由 得2x=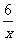 ,
,
y=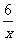
∴x2=3
∴x=±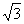 .
.
当x=-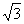 时,y=-2
时,y=-2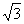 .
.
∴B(-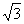 ,-2
,-2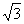 ).
).
Ⅲ.课堂练习
经历将一些实际问题抽象为数学问题的过程,初步学会从数学的角度提出问题。理解问题,并能综合运用所学的知识和技能解决问题.发展应用意识,初步认识数学与人类生活的密切联系及对人类历史发展的作用.
教学重点:用反比例函数的知识解决实际问题.
教学难点:如何从实际问题中抽象出数学问题、建立数学模型,用数学知识去解决实际问题.
教学方法:教师引导学生探索法.
教具准备:多媒体课件
教学过程:
Ⅰ.创设问题情境,引入新课
[师]有关反比例函数的表达式,图象的特征我们都研究过了,那么,我们学习它们的目的是什么呢?
[生]是为了应用.
[师]很好.学习的目的是为了用学到的知识解决实际问题.究竟反比例函数能解决一些什么问题呢?本节课我们就来学一学.
Ⅱ. 新课讲解
某校科技小组进行野外考察,途中遇到片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺垫了若干块木板,构筑成一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时随着木板面积S(m2)的变化,人和木板对地面的压强p(Pa)将如何变化?如果人和木板对湿地地面的压力合计600 N,那么
 (1)用含S的代数式表示p,p是S的反比例函数吗?
(1)用含S的代数式表示p,p是S的反比例函数吗?
为什么?
(2)当木板画积为0.2 m2时.压强是多少?
(3)如果要求压强不超过6000 Pa,木板面积至少要多大?
(4)在直角坐标系中,作出相应的函数图象.
(5)清利用图象对(2)和(3)作出直观解释,并与同伴进
行交流.
[师]分析:首先要根据题意分析实际问题中的两个
变量,然后看这两个变量之间存在的关系,从而去
分析它们之间的关系是否为反比例函数关系,若是
则可用反比例函数的有关知识去解决问题.
请大家互相交流后回答.
[生](1)由p=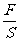 得p=
得p=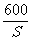
p是S的反比例函数,因为给定一个S的值.对应的就有唯一的一个p值和它对应,根据 函数定义,则p是S的反比例函数.
函数定义,则p是S的反比例函数.
(2)当S=0.2 m2时, p=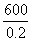 =3000(Pa).
=3000(Pa).
当木板面积为0.2m2时,压强是3000Pa.
(3)当p=6000 Pa时,
 S=
S=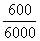 =0.1(m2).
=0.1(m2).
如果要求压强不超过6000 Pa,木板面积至少要0.1 m2.
(4)图象如下:
(5)(2)是已知图象上某点的横坐标为0.2,求该点的纵坐标;
(3)是已知图象上点的纵坐标不大于6000,求这些点所处的
位置及它们横坐标的取值范围.
[师]这位同学回答的很好,下面我要提一个问题,大家知道
反比例函数的图象是两支双曲线、它们要么位于第一、三象限,
要么位于第二、四象限,从(1)中已知p=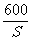 >0,所以图象应位于第一、三象限,为什么这位同学只画出了一支曲线,是不是另一支曲线丢掉了呢?还是因为题中只给出了第一象限呢?
>0,所以图象应位于第一、三象限,为什么这位同学只画出了一支曲线,是不是另一支曲线丢掉了呢?还是因为题中只给出了第一象限呢?
 [生]第三象限的曲线不存在,因为这是实际问题,S不可能取负数,所以第三象限的曲线不存在.
[生]第三象限的曲线不存在,因为这是实际问题,S不可能取负数,所以第三象限的曲线不存在.
[师]很好,那么在(1)中是不是应该有条件限制呢?
[生]是,应为p=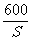 (S>0).
(S>0).
做一做
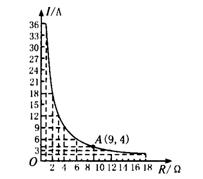
1. 蓄电池的电压为定值.使用此电源时,电流I(A)与电阻
R(Ω)之间的函数关系如下图所示;
(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?
(2)完成下表,并回答问题:如果以此蓄电池为电源的用电
器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内?
|
R/Ω |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
I/A |
|
|
|
|
|
|
4 |
|
[师]从图形上来看,I和R之间可能是反比例函数关系.电压U就相当于反比例函数中的k.要写出函数的表达式,实际上就是确定k(U),只需要一个条件即可,而图中已给出了一个点的坐标,所以这个问题就解决了,填表实际上是已知自变量求函数值.
[生]解:(1)由题意设函数表达式为I=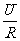
∵A(9,4)在图象上,
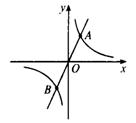 ∴U=IR=36.
∴U=IR=36.
∴表达式为I=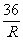 .
.
蓄电池的电压是36伏.
(2)表格中从左到右依次是:12,9,7.2,6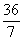 ,4.5,3.6.
,4.5,3.6.
电源不超过10 A,即I最大为10 A,代入关系式中得R=3.6,为最小电阻,所以用电器的可变电阻应控制在R≥3.6这个范围内.
通过对反比例函数的应用,培养学生解决问题的能力.
2.体会数学与现实生活的紧密联系,增强应用意识.提高运用代数方法解决问题的能力
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com