活动一　操作与思考

　 如图，点A在⊙O外，点B₁ 、B₂　、B₃在⊙O上，点C在⊙O内，度量∠A、∠B₁ 、∠B₂　、∠B₃、∠C的大小，你能发现什么？　　

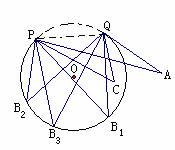
∠B₁ 、∠B₂　、∠B₃有什么共同的特征？

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

归纳得出结论，顶点在_______，并且两边________________________的角叫做圆周角。

强调条件：①_______________________，②___________________________。

识别图形：判断下列各图中的角是否是圆周角？并说明理由．

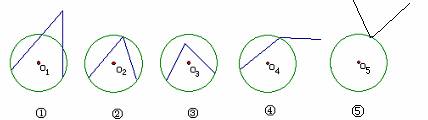
活动二　观察与思考

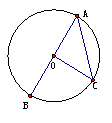
如图，AB为⊙O的直径，∠BOC、∠BAC分别是BC所对的圆心角、圆周角，求出图(1)、(2)、(3)中∠BAC的度数．

通过计算发现：∠BAC＝＿＿∠BOC．

试证明这个结论：

活动三　思考与探索

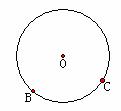
1.如图，BC所对的圆心角有多少个？BC所对的圆周角有多少个？请在图中画出BC所对的圆心角和圆周角，并与同学们交流。

9.人们常用“一字之差，差之千里”来形容因一点小小的差别，往往会给问题本身带来很大的区别。在数学中，这样的例子比比皆是，下面两句话，先请你找出其中微小的区别，然后再比较解决问题的结果：

(1)在⊙O中，一条弧所对的圆心角是120°，该弧所对的圆周角是多少度？

(2)在⊙O中，一条弦所对的圆心角是120°，该弦所对的圆周角是多少度？

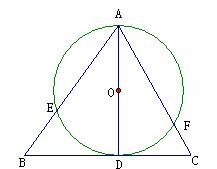
8.已知，如图，AD是△ABC的边BC上的高，以AD为直径作圆，与AB、AC分别相交于点E、F，求证：AE·AB=AF·AC

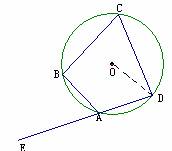
7.如图，四边形ABCD的顶点都在⊙O上，点E在DA延长线上，且BAD的度数为130 °，求∠BAE的度数。

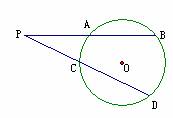
6.如图，是否都能求证出PA·PB=PC·PD？

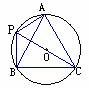
5.如图，AB、AC是⊙O中相等的两弦，延长CA到点D，使AD=AC，连接DB并延长交⊙O于点E，连接CE，求证：CE是⊙O的直径。

4.已知，如图，△ABC的顶点都在⊙O上，点P在⊙O上，且∠APC=∠CPB=60°.求证：△ABC是等边三角形.

3.如图，OA、OB、OC都是⊙O的半径，∠AOB＝2∠BOC，探索∠ACB与∠BAC之间的数量关系？并说明理由.

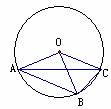
2.如图，AB、AC分别是⊙O的直径和弦，∠BAC＝30°,OD⊥AB，与AC相交于点D，OD=5cm，求弦AC的长.

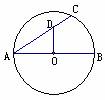
1.如图，OA是⊙O的半径，以OA为直径的⊙C与⊙O的弦AB相交于点D，

求证：D是AB的中点.