2、请你根据图3.4-11中三视图，想象物体的形状，用小正方块搭出这个物体，并数一数有多少个小正方块。

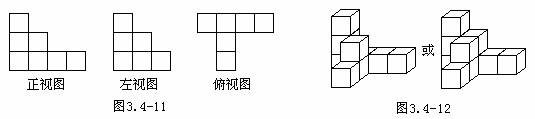
答：物体的立体图如3.4-12所示。

思路点拨：我们先确定前后称为行，左右称为列，上下称为层。由正视图确定每一列的最高层数，由左视图确定每一行的最高层数，由俯视图确定行与列的分布。

易错辨析：空间想象是小正方体的位置易错。

方法点评：在想象出物体的立体图形后再根据立体图画三视图。

[课外链接]

图3.4-13是一个有若干个小正方体搭成的几何体的俯视图，其中小正方形格内的数字是小正方体的层数，请你画出它的正视图和左视图。

思路点拨：从俯视图可以看出有三行，四列，以及每行(每列)的最高层数。因而在正视图中共四列，(自左到右数)第一列最高一层，第二列最高两层，第三列最高三层，第四列最高一层，从而确定正视图。在左视图中共三行，(自左到右数)第一行最高三层，第二行最高两层，第三行最高一层，从而确定左视图。正视图和左视图如图3.4-14所示。

[随堂演练]

1、如图3.4-9是一个物体的三视图，试说出该物体的形状。

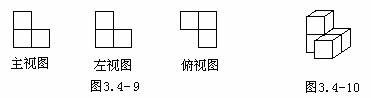
答：该物体的形状如图3.4-10。

思路点拨：在想象立体图形前，利用一定数量的物体实例观察，发现三个方向上所看到的物体的特征，为脱离实体进行想象打下基础。

易错辨析：空间想象时的三个方向可能不到位。

方法点评：在根据三视图画立体图形时，一定要充分发挥自己的空间想象力。并且要注意由三视图想象实物图时可能不唯一。

5.4　 从三个方向看(第二课时)

[新知导读]

一个物体的三视图如图3.4-7所示，画出该物体的立体图形。

答：该物体的立体图形如图3.4-8所示。

[范例点睛]

5.4从三个方向看(2)

题目 5.4从三个方向看(2) 教学目标 会画一些简单物体的三视图，并能根据三视图，想象一些简单物体的形状，进一步感知立体图形与平面图形的关系 教学重点 根据三视图想象物体的形状 教学难点 根据三视图想象物体的形状 教学方法 引导发现式 教学工具 四棱柱，四棱锥，圆柱 教学内容 教师活动 学生活动

根据三视图说出相应几何体的名称 长方体　　　　　　　　　　 圆柱 　 由6个小立方体搭成一个几何体，它的主视图与左视图如下 4种情况 根据三视图用小立方体搭出这个物体 　　 根据三视图想象物体的形状 练习：P102 1,2 作业：4，5，6 　　 　 思考 讨论 　 　 　 　 　 　 　 　 　 　 　 动手 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 观察思考

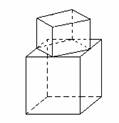
7、大小两个正方体叠成如图所示几何体，请作出它的三视图。

6、若一个立体图形的正视图与左视图都是等腰三角形，俯视图是圆，则这个图形可能是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 　)

A、圆台　　　 B、圆柱　　　 C、圆锥　　　　 D、三棱锥

5、如图，是一个立体图形的三视图，这个立体图形是由一些相同的小正方体构成，这些相同的小正方体的个数是　　　　　　　　　　　　　　　　　　　　　　 (　　 )

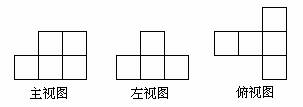
A、4个　　　 B、5个　　　 C、6个　　　　 D、7个

4、一物体的三视图如下图，你能描述该物体的形状吗？

3、画出下列几何体的三视图：

2、正方体的主视图、左视图、俯视图均为　　　　　　　　 。