活动1

举出生活中的平移的现象：火车、电梯、飞机等，并用计算机演示．

学生倾听、理解、想象和欣赏．

活动2

问题1：请你举出一些生活中的平移现象．

问题2：什么样的变化才是平移？

学生活动设计：

学生可以分组讨论，举例，其他人辨别是否是平移现象，然后通过自己举的事例来归纳和总结平移的含义．

学生归纳：

平移：图形的平行移动就是平移．

大小和方向都不变．

决定因素：方向和距离．

让学生充分讨论，辨别自己的判断，同学间进行交流．

活动3

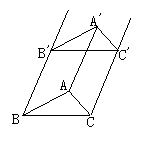
把一个三角形ABC，移到三角形A′B′C′的位置．你能理解下列概念吗？

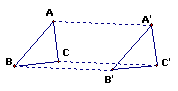(1)对应点；(2)对应线段．

学生活动设计：

学生观察图形，可以发现经过平移能够互相重合的点

就是对应点，对应点的连线就是对应线段．

教师活动设计：

教师在此环节主要让学生学会观察，学会分析两个图形之间的关系，引导学生发现经过变换后能够互相重合的元素就是对应元素．

因此，上述平移中，对应点是A与A′，B与B′，C与C′；

　　　　　　　　　 对应线段是AB与A′B′，BC与B′C′，AC与A′C′．

2.把鱼往左平移8cm.(假设每小格是1cm2)

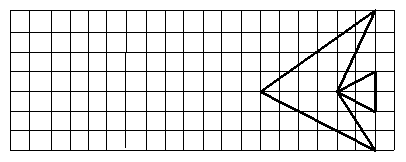
1.下列图案可以由什么图形平移形成.

(1)

(2)

3.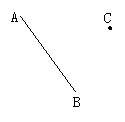线段AB是线段CD平移后得到的图形.点A为点C的对应点,说出点B的对应点D的位置:____________.

2.经过平移,每一组对应点所连成的线段________.

1.图形经过平移后,_______图形的位置,________图形的形状,________图形的大小.(填“改变”或“不改变”)

2.补充作业:

5.例题讲解.

　　 例:如图(4)-1,平移三角形ABC,使点A移动到点A′.画出平移后的三角形A′B′C′.

教师:“点A移到点A′”这句话告诉我们图形平移的方向是A到A′的方向， 平移的距离为线段AA′的长，根据这两个要素就可以确定点B、C的对应点B′、C′，从而画出△A′B′C′.

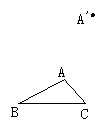
　　　　　　　　　　 (4)-1　　　　　　　　 (4)-2

　　 解:如图(4)-2,连接AA′,分别过B、C作AA′的平行线L、L′,在L上截取BB ′=AA′,在L′上截取CC′=AA′,连接A′C′,A′B′,B′C′.则△A′B′C ′为所求画的三角形.

4.给出平移的定义.

　　 定义:一个图形沿着某个方向移动一定的距离,图形的这种移动,叫做平移变换,简称平移.

　　 教师以课本图5.4-1上排左图为例解说:

　　 把“基本图形”说成“橄榄形”.第一排左边的“橄榄形”沿着水平方向向左平移一个正方形边长的距离得第二个“橄榄形”，平移二个正方形边长的距离得第三个“橄榄形”……要想平移得第二批的“橄榄形”，平移的方向不再是水平方向，每一次平移时，方向在变化、平移的距离也在变化.

　　 关于平移的方向,可结论课本图5.4-5说明图形平移方向,不一定是水平的.

　教师引导学生举出生活一引进利用平移的例子, 如人在电梯上两个不同时刻之间的位置关系,坐登山缆车人在吊箱里两个不同时刻的位置关系都是平移;黑板报中花边设计利用了平移,奥运会五环旗图案五环之间通过平移得到……