7、定点P在直线AB外，动点O在直线AB上移动，当PO最短时，∠POA=_______，这时线段PO所在的直线是AB的___________，线段PO叫做直线AB的______________。

6、如图4，已知AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF，若∠1=50°，则∠2的度数为_______________。

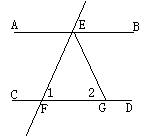
　 　　　 图4

5、把命题“等角的余角相等”改写成“如果……，那么……”的形式是_________________。

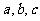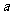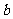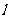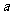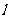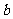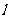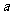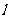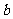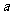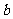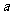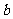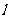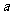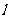4、设为平面内三条不同的直线，①若∥，⊥，则与的位置关系是______；②若⊥，⊥，则与的位置关系是___________；③若∥，∥，则与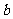的位置关系是____________。

3、如图3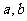，直线与直线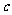相交，给出下列条件：①∠1=∠2；②∠3=∠6；③∠4+∠7=180°；④∠5+∠3=180°，其中能判断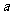∥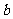的是_______________(填序号)。

1、如图1，计划把河水引到水池A中，可以先引AB⊥CD，垂足为B，然后沿AB开渠，则能使所开的渠最短，这样设计的依据是________________。

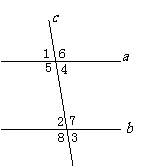　 2、如图2，AB∥CD，∠1=39°，∠C和∠D互余，则∠D=________，∠B=________。

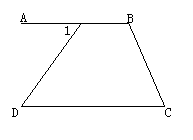
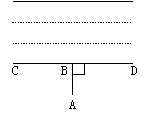
　　　　　　　　 图1　　　　　　　 图2　　　　　　　　　　 图3

小结：

平移特征：

(1)图形形状、大小不变；

(2)连接对应点连线平行且相等．

作业：

习题5.4．

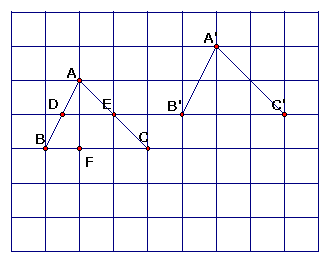
问题1：如图，△ABC平移到△A′B′C′的位置．

(1)请指出平移的距离和方向．

(2)点D、E、F经过平移到了什么位置？

问题2：如图，将△ABC先下移2个格再右移4个格得到△A′B′C′．

问题3：图案设计，根据如图所示的图形，通过平移设计一个图案．

学生活动设计：

以上三个问题，由学生自主探索，自主设计，找到解决问题的方法，从而进一步体会平移在作图中的应用，同时感受平移变化的特征．

教师活动设计：

鼓励学生解决问题，在进行图案设计时，鼓励学生充分发挥自己的想象力．

(解答)．

问题1(1)平移的方向是A－A′方向，距离是AA′的长度．

　　　 (2)如下右图．

问题2：如上左图．

问题3：略．

问题4：如图，平移△ABC，使点A移动到点A′，画出平移后的△A′B′C′．

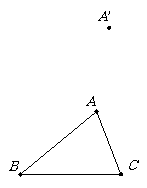
分析：图形平移后的对应点有什么特征？作出点B和点C的对应点B′和C′，能确定△A′B′C′吗？(课件：平移三角形.gsp)

解答：如图，连接AA′，过点B作AA′的平行线l，在l上截取BB′＝AA′，则点

B′就是点B的对应点．

类似地，你能作出点C的对应点C′，并进一步得到平移后的三角形A′B′C′吗？

2．对应点所连线段平行且相等(都是平移的距离)．

教师活动设计：

此时要鼓励学生大胆猜测，引导学生归纳出平行的特征．

活动4

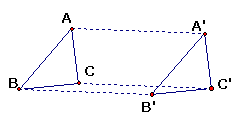如图△ABC经过平移成为△A′B′C′，在这个变化过程中，你能得到哪些量是不变的？除了这些量不变外，你还能发现哪些结论？

学生活动设计：

学生通过画图、度量进行猜测，得出下列结论

结论：

1．　 对应线段平行且相等；

(相等、平行因为是平移，是图形的平行移动)；