
2、两条直线的位置关系
在同一平面内,两条直线的位置关系只有两种:⑴相交;⑵平行。
因此当我们得知在同一平面内两直线不相交时,就可以肯定它们平行;反过来也一样(这里,我们把重合的两直线看成一条直线)
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合(因为两点确定一条直线)
1、平行线的概念:
在同一平面内,不相交的两条直线叫做平行线,直线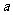 与直线
与直线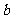 互相平行,记作
互相平行,记作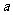 ∥
∥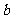 。
。
5.2平行线
5、如何理解“垂线”、“垂线段”、“两点间距离”、“点到直线的距离”这些相近而又相异的概念
分析它们的联系与区别
⑴垂线与垂线段 区别:垂线是一条直线,不可度量长度;垂线段是一条线段,可以度量长度。 联系:具有垂直于已知直线的共同特征。(垂直的性质)
⑵两点间距离与点到直线的距离 区别:两点间的距离是点与点之间,点到直线的距离是点与直线之间。 联系:都是线段的长度;点到直线的距离是特殊的两点(即已知点与垂足)间距离。
⑶线段与距离 距离是线段的长度,是一个量;线段是一种图形,它们之间不能等同。
4、点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
记得时候应该结合图形进行记忆。
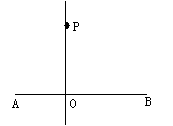
如图,PO⊥AB,同P到直线AB的距离是PO的长。PO是垂线段。PO是点P到直线AB所有线段中最短的一条。
现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用。
3、垂线的画法:
⑴过直线上一点画已知直线的垂线;⑵过直线外一点画已知直线的垂线。
注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线;②过一点作线段的垂线,垂足可在线段上,也可以在线段的延长线上。
画法:⑴一靠:用三角尺一条直角边靠在已知直线上,⑵二移:移动三角尺使一点落在它的另一边直角边上,⑶三画:沿着这条直角边画线,不要画成给人的印象是线段的线。
2、垂线
⑴定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
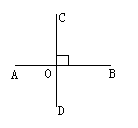 符号语言记作:
符号语言记作:
如图所示:AB⊥CD,垂足为O
⑵垂线性质1:过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记)
⑶垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。简称:垂线段最短。
1、邻补角与对顶角
两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:
|
|
图形 |
顶点 |
边的关系 |
大小关系 |
|
对顶角 |
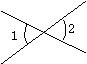 ∠1与∠2 |
有公共顶点 |
∠1的两边与∠2的两边互为反向延长线 |
对顶角相等 即∠1=∠2 |
|
邻补角 |
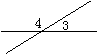 ∠3与∠4 |
有公共顶点 |
∠3与∠4有一条边公共,另一边互为反向延长线。 |
∠3+∠4=180° |
注意点:⑴对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;
⑵如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角
⑶如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角。
⑶两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
5.1相交线
4.在方格纸上,利用平移画出长方形ABCD的立体图,其中点D′是D的对应点.(要求在立体图中,看不到的线条用虚线表示)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com