
4、平行线的性质与判定
①平行线的性质与判定是互逆的关系
 两直线平行 同位角相等;
两直线平行 同位角相等;
两直线平行 内错角相等;
两直线平行 同旁内角互补。
其中,由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质。
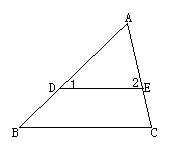 典型例题:已知∠1=∠B,求证:∠2=∠C
典型例题:已知∠1=∠B,求证:∠2=∠C
证明:∵∠1=∠B(已知)
∴DE∥BC(同位角相等,
两直线平行)
∴∠2=∠C(两直线平行
同位角相等)
注意,在了DE∥BC,不需要再写一次了,得到了DE∥BC,这可以把它当作条件来用了。
典型例题:如图,AB∥DF,DE∥BC,∠1=65°
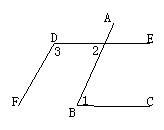 求∠2、∠3的度数
求∠2、∠3的度数
解答:∵DE∥BC(已知)
∴∠2=∠1=65°(两直线平行,内错角相等)
∵AB∥DF(已知)
∴AB∥DF(已知)
∴∠3+∠2=180°(两直线平行,同旁内角互补)
∴∠3=180°-∠2=180°-65°=115°
3、命题:
⑴命题的概念:
判断一件事情的语句,叫做命题。
⑵命题的组成
每个命题都是题设、结论两部分组成。题设是已知事项;结论是由已知事项推出的事项。命题常写成“如果……,那么……”的形式。具有这种形式的命题中,用“如果”开始的部分是题设,用“那么”开始的部分是结论。
有些命题,没有写成“如果……,那么……”的形式,题设和结论不明显。对于这样的命题,要经过分析才能找出题设和结论,也可以将它们改写成“如果……,那么……”的形式。
注意:命题的题设(条件)部分,有时也可用“已知……”或者“若……”等形式表述;命题的结论部分,有时也可用“求证……”或“则……”等形式表述。
2、两条平行线的距离
如图,直线AB∥CD,EF⊥AB于E,EF⊥CD于F,则称线段EF的长度为两平行线AB与CD间的距离。
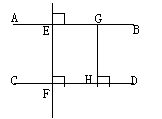
注意:直线AB∥CD,在直线AB上任取一点G,过点G作CD的垂线段GH,则垂线段GH的长度也就是直线AB与CD间的距离。
1、平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
 性质3:两直线平行,同旁内角互补。
性质3:两直线平行,同旁内角互补。
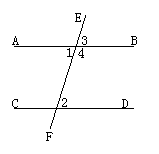
几何符号语言:
∵AB∥CD
∴∠1=∠2(两直线平行,内错角相等)
∵AB∥CD
∴∠3=∠2(两直线平行,同位角相等)
∵AB∥CD
∴∠4+∠2=180°(两直线平行,同旁内角互补)
5.3平行线的性质
7、两直线平行的判定方法
方法一 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
简称:同位角相等,两直线平行
方法二 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
简称:内错角相等,两直线平行
方法三 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
 简称:同旁内角互补,两直线平行
简称:同旁内角互补,两直线平行
几何符号语言:
∵ ∠3=∠2
∴ AB∥CD(同位角相等,两直线平行)
∵ ∠1=∠2
∴ AB∥CD(内错角相等,两直线平行)
∵ ∠4+∠2=180°
∴ AB∥CD(同旁内角互补,两直线平行)
请同学们注意书写的顺序以及前因后果,平行线的判定是由角相等,然后得出平行。平行线的判定是写角相等,然后写平行。
注意:⑴几何中,图形之间的“位置关系”一般都与某种“数量关系”有着内在的联系,常由“位置关系”决定其“数量关系”,反之也可从“数量关系”去确定“位置关系”。上述平行线的判定方法就是根据同位角或内错角“相等”或同旁内角“互补”这种“数量关系”,判定两直线“平行”这种“位置关系”。
⑵根据平行线的定义和平行公理的推论,平行线的判定方法还有两种:①如果两条直线没有交点(不相交),那么两直线平行。②如果两条直线都平行于第三条直线,那么这两条直线平行。
典型例题:判断下列说法是否正确,如果不正确,请给予改正:
⑴不相交的两条直线必定平行线。
⑵在同一平面内不相重合的两条直线,如果它们不平行,那么这两条直线一定相交。
⑶过一点可以且只可以画一条直线与已知直线平行
解答:⑴错误,平行线是“在同一平面内不相交的两条直线”。“在同一平面内”是一项重要条件,不能遗漏。
⑵正确
⑶不正确,正确的说法是“过直线外一点”而不是“过一点”。因为如果这一点不在已知直线上,是作不出这条直线的平行线的。
典型例题:如图,根据下列条件,可以判定哪两条直线平行,并说明判定的根据是什么?

解答:⑴由∠2=∠B可判定AB∥DE,根据是同位角相等,两直线平行;
⑵由∠1=∠D可判定AC∥DF,根据是内错角相等,两直线平行;
⑶由∠3+∠F=180°可判定AC∥DF,根据同旁内角互补,两直线平行。
6、如何判别三线八角
判别同位角、内错角或同旁内角的关键是找到构成这两个角的“三线”,有时需要将有关的部分“抽出”或把无关的线略去不看,有时又需要把图形补全。
 例如:
例如:
|
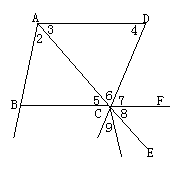
如图,判断下列各对角的位置关系:⑴∠1与∠2;⑵∠1与∠7;⑶∠1与∠BAD;⑷∠2与∠6;⑸∠5与∠8。
我们将各对角从图形中抽出来(或者说略去与有关角无关的线),得到下列各图。
如图所示,不难看出∠1与∠2是同旁内角;∠1与∠7是同位角;∠1与∠BAD是同旁内角;∠2与∠6是内错角;∠5与∠8对顶角。
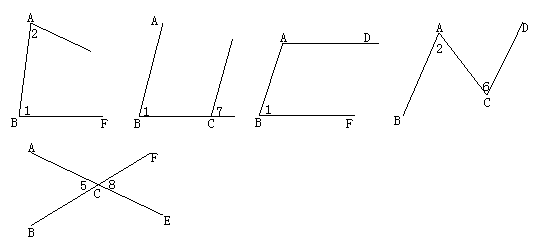
注意:图中∠2与∠9,它们是同位角吗?
不是,因为∠2与∠9的各边分别在四条不同直线上,不是两直线被第三条直线所截而成。
5、三线八角
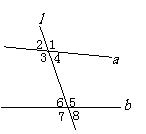 两条直线被第三条直线所截形成八个角,它们构成了同位角、内错角与同旁内角。
两条直线被第三条直线所截形成八个角,它们构成了同位角、内错角与同旁内角。
如图,直线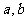 被直线
被直线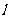 所截
所截
①∠1与∠5在截线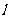 的同侧,同在被截直线
的同侧,同在被截直线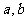 的上方,
的上方,
叫做同位角(位置相同)
②∠5与∠3在截线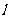 的两旁(交错),在被截直线
的两旁(交错),在被截直线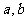 之间(内),叫做内错角(位置在内且交错)
之间(内),叫做内错角(位置在内且交错)
③∠5与∠4在截线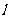 的同侧,在被截直线
的同侧,在被截直线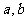 之间(内),叫做同旁内角。
之间(内),叫做同旁内角。
④三线八角也可以成模型中看出。同位角是“A”型;内错角是“Z”型;同旁内角是“U”型。
4、平行公理的推论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
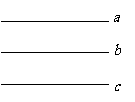
如左图所示,∵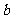 ∥
∥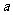 ,
,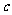 ∥
∥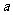
∴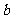 ∥
∥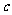
注意符号语言书写,前提条件是两直线都平行于第三条直线,才会结论,这两条直线都平行。
3、平行公理――平行线的存在性与惟一性
经过直线外一点,有且只有一条直线与这条直线平行
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com