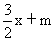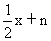2、已知一次函数y＝和y＝－的图象交于点A(－2,0)，与y轴分别交于B、C两点，那么△ABC的面积为　　　 。

1、直线y＝x+3与y＝－3x－1的交点坐标为　　　　　 。

2、书P162/习题1、2

1、书P162/练习1、2

例1、(1)在同一个直角坐标系中，画出一次函数y＝2x+3和y＝的图象，并在图象中标出交点坐标。

(2)求二元一次方程组　 2x－y+3＝0　 的解。

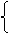　　　　　　　　　　　　 X－2y－3＝0

(3)交点坐标与方程组的解有关系吗？什么关系？请说明理由。

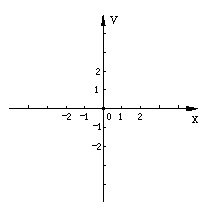
例2、利用一次函数图象解二元一次方程组　 x+2y＝4

　　　　　　　　　　　　　　　　　　　　 2x－y＝3。

例3、(1)已知函数y＝kx+1与y＝－0.5x+b的图象交于点(2,5)，求k、b的值。

(2)求一次函数y＝4x－4与y＝－x+6的交点坐标。

2、一般地，一次函数y＝kx+b图象上任意一点的　　　 都是二元一次方程kx－y+b＝0的一个解；以二元一次方程kx－y+b＝0的解为　　　　　　 都在一次函数y＝kx+b的图象上。

1、把二元一次方程2x-y-3=0写成一次函数y＝　　　　　 ；把一次函数写成二元一次方程为

　　　　　　　 。

2、平移的特征：

　①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等，对应角相等，图形的形状与大小都没有发生变化。

　②经过平移后，对应点所连的线段平行(或在同一直线上)且相等。

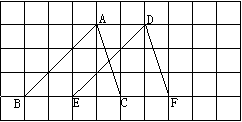典型例题：如图，△ABC经过平移之后成为△DEF，那么：

⑴点A的对应点是点＿＿＿＿＿＿＿＿＿；⑵点B的对应点是点＿＿＿＿＿＿。

⑶点＿＿＿＿＿的对应点是点F；⑷线段AB的对应线段是线段＿＿＿＿＿＿＿；

⑸线段BC的对应线段是线段＿＿＿＿＿＿＿；⑹∠A的对应角是＿＿＿＿＿＿。

　⑺＿＿＿＿的对应角是∠F。

解答：

　⑴D；⑵E；⑶C；⑷DE；⑸EF；⑹∠D；⑺∠ACB。

思维方式：利用平移特征：平移前后对应线段相等，对应点的连线段平行或在同一直线上解答。

1、平移变换

　①把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同。

　②新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点

　③连接各组对应点的线段平行且相等

5.4平移