
4. 在平面直角坐标系中,有点P(2,1),Q(2,5),在y轴上取一点R(0,m),当m为何值时,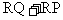 有最小值?
有最小值?
3. 甲船在某港口东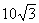 海里,北10海里,乙船在同港口西5海里,北
海里,北10海里,乙船在同港口西5海里,北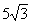 海里,建立直角坐标系,求出甲、乙两船之间的距离。
海里,建立直角坐标系,求出甲、乙两船之间的距离。
2. 选择题。
(1)若点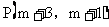 在直角坐标系的x轴上,则P点坐标为( )
在直角坐标系的x轴上,则P点坐标为( )
A. (0,-2) B. (2,0)
C. (4,0) D. (0,-4)
(2)在直角坐标系中,适合条件 的点P(x,y)的个数为( )
的点P(x,y)的个数为( )
A. 1 B. 2 C. 4 D. 8
1. 填空题。
(1)已知点A(-3,2),它与x轴的距离为_____________,它与y轴的距离为_____________。
(2)已知点P(x,y),如果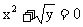 ,那么点P的位置在_____________。
,那么点P的位置在_____________。
(3)在直角坐标系中有点A在原点O北偏东30°方向上,且距离原点6个单位长度,则点A的坐标为_____________。
4. 坐标平移公式
若M点的坐标为(x,y),将M点平移到M'点的坐标为(x',y'),则
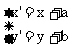
其中,当a>0时,M点向右平移a个单位到M'
当a<0时,M点向左平移|a|个单位到M'
当b>0时,M点向上平移b个单位到M'
当b<0时,M点向下平移|b|个单位到M'
[典型例题]
例1. 已知两点A(0,2),B(4,1),点P是x轴上一点,求PA+PB的最小值。
解:如图1,作B点关于x轴的对称点B',连AB',交x轴于点P,又作B'C⊥y轴于C
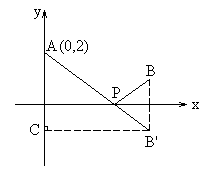
图1
由平面几何知识知,这时PA+PB最小,且等于AB'的长度
∵B与B'关于x轴对称
∴B'的坐标为(4,-1)
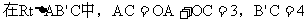
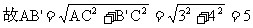
∴PA+PB的最小值为5
说明:若在Rt△ABC中,两直角边长为a,b,斜边长为c,则有c2=a2+b2。
例2. 在直角坐标系xOy中,已知点A、C坐标分别为A(-2,0),C(0,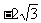 ),在坐标平面xOy内,是否存在点M,以AC为等腰△ACM的一边,且底角为30°,如果存在,请直接写出符合条件的点M的坐标,如果不存在,请说明理由。
),在坐标平面xOy内,是否存在点M,以AC为等腰△ACM的一边,且底角为30°,如果存在,请直接写出符合条件的点M的坐标,如果不存在,请说明理由。
解:如图2
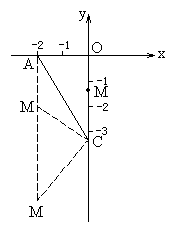
图2
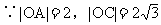
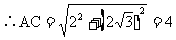
(1)以AC为底时,|AM|=|MC|,令M的坐标为(0,y)或(-2,y)


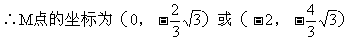
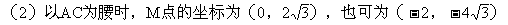
故满足条件的M点的坐标为:

说明:设A(x1,y1),B(x2,y2),则两点A、B之间的距离公式为:
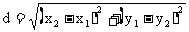
例3. 等腰直角△ABC的直角顶点C在y轴上,斜边AB在x轴上,且点A在点B的左
解:由题意知,C点既可能在y轴的正半轴,也可能在y轴的负半轴,由此我们可作出草图,C1、C2分别表示两个点C的可能位置(见图3)。
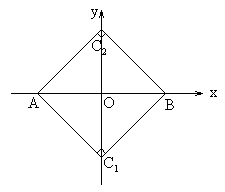
图3


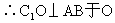
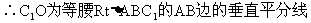
∴A、B关于点O对称
又∵A点在B点左侧
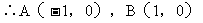
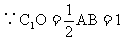
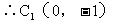
根据题意及图形,C1与C2关于O对称
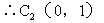
即点C的坐标为(0,-1)或(0,1)
例4. 如图4所示,在平面直角坐标系中,A(-3,4),B(-1,-2),点O为坐标原点,点C、D分别是点A、B关于y轴的轴反射的像,求图中阴影部分的面积。
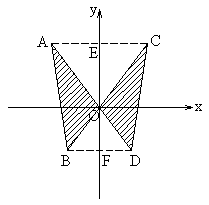
图4
解:连结AC、BD,分别与y轴相交于点E、F
方法一:因为点A、C关于y轴对称,且A(-3,4)
∴点C的坐标为(3,4),且AC=6
∵点B、D关于y轴对称,且B(-1,-2)
∴点D的坐标为(1,-2),且BD=2
又∵根据轴反射的性质可知:
AC、BD都与y轴垂直,则垂足E、F的坐标分别是(0,4),(0,-2)
∴EF=6

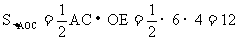
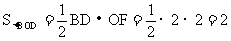
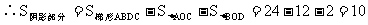
方法二:∵点A与C,点B与D都关于y轴对称
∴AC⊥y轴,BD⊥y轴
又∵A(-3,4),B(-1,-2)
∴点E、F的坐标分别为(0,4),(0,-2)
∴AE=3,BF=1,且EF=6
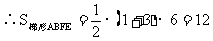
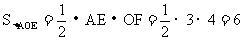
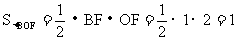
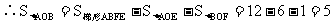
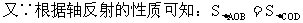
[模拟试题](答题时间:25分钟)
3. 坐标平面内的点与有序实数对的一一对应关系
有序实数对(x,y)与平面内的点构成一一对应的关系。
2. 坐标轴上的点及各种对称点的坐标特征。
(1)坐标轴上的点的坐标特征
x轴上的点,纵坐标为0,可记为(x,0)
y轴上的点,横坐标为0,可记为(0,y)
原点O的坐标为(0,0)
(2)对称点的坐标特征
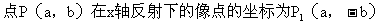
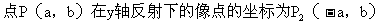
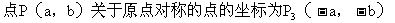
(3)平行于坐标轴的直线的坐标特征
平行于x轴的直线上的任意两点,纵坐标相同。
平行于y轴的直线上的任意两点,横坐标相同。
1. 平面直角坐标系:
在平面内画两条互相垂直且有公共原点的数轴,这样就组成了平面直角坐标系。
说明:一般把一条画成水平的,取向右的方向为正方向,称它为x轴或横轴。
一条画成铅直的且取向上的方向为正方向,称它为y轴或纵轴。
2. 难点:
根据具体问题建立合适的平面直角坐标系,确定点的位置或描述点的坐标。
1. 重点:
认识并画出平面直角坐标系;建立适当的直角坐标系,描述物体的位置,能根据点的位置写出坐标,根据坐标描出点的位置。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com