6．　 已知A(－1，0)，B(x，0)且AB＝2，则x＝　　　　 .

5．　 点P(4，－3)到x轴的距离是　　　　　　 ，到y轴的距离是　　　　 .

4．　 若点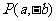在第二象限，则点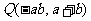在第　　　　　 象限；

3．　 已知点P的坐标为(2 – a，3a + 6)，且点P到两坐标轴的距离相等，则点P坐标是　　　　　　 .

2．　 若点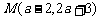是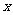轴上的点，则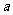的值是　　　　　　　　 .

1．　 如果点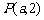在第二象限，那么点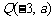在　　　　　 .

2.　　　　 对于任意一对有序数对，坐标平面内有唯一的一点与它对应.也就是说，坐标平面内的点与有序数对是-一对应的.

n　　　　 检测评估

1.　　　　 对于坐标平面内任意一点，有唯一的一对有序数对与它对应；

3. 在直角坐标系中,点M(1，2)可由点N(1，0)怎样平移得到?

n　　　　 学法指导

²　　 引领激活　

很多同学都看过这部影片，那么你知道“泰坦尼克”遭遇不幸时是如何向救援人员报告他们所处的具体位置？你知道最好的和最常用的方法是什么？

²　　 范例点评　

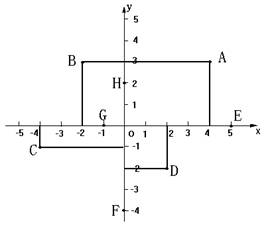
[例1　]在直角坐标系中，描出下列各点：

A(4，3)，B(-2，3)，C(-4，-1)，D(2，-2).

问：如果点在坐标轴上，这个点的坐标是怎样的？

写出图中E、F、G、H、O各点的坐标.

解：E(5，0)，F(0，-4)，G(-1，0)，H(0，2)，O(0，0).

评注：对于坐标平面内任意一点M，都有唯一的一对有序实数(x，y)和它对应；对于任意一对有序实数(x，y)，在坐标平面内都有唯一的点M和它对应.即：坐标平面内的点与有序实数对是一一对应的.

[例2] 　指出下列各点所在的象限或坐标轴：A(-2，3)；B(1，-2)；C(-1，-2)；D(3，2)；E(-3，0)；F(0，1)．

分析：要解决这个问题，首先要画出直角坐标系，描出给出的各点；然后，按照图中所描的点的位置，给出答案．

提问：题中为什么要写出“所在的象限或坐标轴”？明确坐标轴上的点不属于任何象限．

由学生完成例题之后，然后探究：

(1)坐标轴上的点的坐标有什么特征？

(2)各象限中点的坐标有何特征？根据点所在象限，用“+．-”号填表：

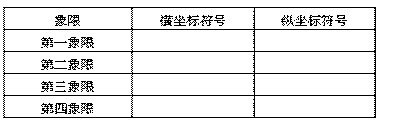
提问：任一点P(x，y)

(1)如果P(x，y)在第二象限，那么x，y分别是正数还是负数？

(2)如果x＞0，y＜0，P(x，y)在第几象限？通过这两个问题，使学生能从正、反两个方面理解坐标平面内点的坐标的特征．

n　　　　 师生互动

²　　 课堂交流

在坐标平面内不同的点的坐标是否相同？不同的坐标所表示的点是否相同？那么点的坐标是用什么表示的？

²　　 误区警示

2. 在直角坐标系中，点P(3，5)在第　　　　 象限.