1、平面直角坐标系的引入

　　 对于上述第(2)个问题，我们可以用图3来表示： 这时，小兵(P)的位置就可以用两个数来表示．如点P离AB边1 cm，离AD边1. 5 cm，如果1 cm代表20 m，那么小兵离AB边20 m，离AD边30 m.

　　 对于上述第(3)个问题，我们是否也可以借助于这样的一些线来确定小兵的位置呢？我们在小兵所在的平面内画上一些方格线(如图4)，利用上节课所学的知识，就可以解决这个问题了．

(然后由学生回答这个问题的解决过程)

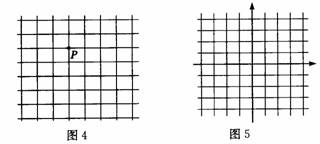
受上述方法的启发，为了确定平面内点的位置，我们可以画一些纵横交错的直线，便于标记每一条直线的顺序，我们又可以以其中的两条为基准(如图5).

　　 最早采用这种方法的是法国数学家笛卡儿，然后向学生简要介绍笛卡儿的有关故事．

2、如果我们画一条数轴，取小红的位置为原点，取向右的方向为正方向，取两盏路灯间的距离为一个单位长度，那么小华的位置(A)就可以用－3来表示，小明的位置(B)就可以用6来表示(如图2).此时，我们说点A在数轴上的坐标是－3，点B在数轴上的坐标是6．这样数轴上的点的位置与坐标之间就建立了对应关系．

设计意图：将数轴上点的坐标的概念学习置于具体的问题情境中。

　　 问题：(1)在上述情境中，如果小兵位于小明左侧的第二盏路灯处，你能说出小兵在数轴上对应的点的坐标吗？

　　 (2)如果小兵站在一个长方形的操场上，你用什么方法可以确定小兵的位置？

(3)如果小兵站在一个大操场上，你用什么方法可以确定小兵的位置？

设计意图：三个问题的安排有一定的层次性，为下一步引出平面直角坐标系作铺垫。

1、在一条笔直的街道边，竖着一排等距离的路灯，小华、小红、小明的位置如图1所示，你能根据图示确切地描述他们三个人的位置关系吗？

在学生进行叙述后，教师可以抓住以什么为“基准”，并借助于数轴来处理这个问题，从而进入课题．

设计意图：学生可以以其中的一人为基准进行描述，其目的是为数轴上的点的坐标的确定做准备。

6．1.2　 平面直角坐标系

温故知新　　 1.略　 2. 第一象限　 3.由M下向平移2个单位得到.

引领激活　 由学生熟悉的地理知识，最好的和最常用的方法－－－－－报告经纬度(34oW，45oN)，救援人员就根据(34oW，45oN)这一对实数找到了出事的位置，抽象得出用一对实数来表示平面内点的位置的数学问题。

课堂交流　 坐标平面内不同的点的坐标不相同,不同的坐标所表示的点也不相同,点的坐标用有序数对表示.

检测评估　　　 1.第三象限　 2. 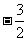　3.-1或-4　 4.第二象限　 5.3　 4　 6.-3或1　 7.D　 8.略　 9.略 10.略　 11.直角坐标系内每一个点均可用有序数对表示,每一有序数对都能在平面直角坐标系上找出与之对应的一个点.　 12.略.

12.自己建立一个直角坐标系，然后在你建立的坐标系中画一个多边形，请你的同伴写出每一个点的坐标，然后你加以评判.

11.思考“直角坐标系内的点与所有的有序数对是一一对应的”这一句话的含义.

10.总结每个象限内的点坐标的符号特点.

9.以“我眼中的坐标系”为题写一篇数学周记.

8.(2003年徐州)在平面直角坐标系中，已知点A(1，6)、B(2，3)、C(3，2)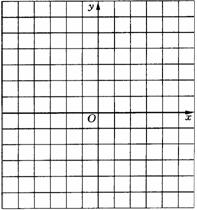．⑴ 在下面的平面直角坐标系中描出点A、B、C.

以下为研究性作业

7. (2003年南通)若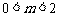，则点p在[　　 ].

A、第一象限　　　　　 B、第二象限　　　　 C、第三象限　　　　　 D、第四象限