2、平面直角坐标系的有关概念；

1、平面直角坐标系的作用；

教材第49页“练习”第1题。

1、坐标轴上点的坐标

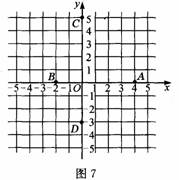
　　 问题：(1)在图7的平面直角坐标系中，你能分别说出点A，B，C，D的坐标是什么吗？

　　 (2)从上面的练习中你有什么发现？原点O的坐标是什么？x轴和y轴上的点的坐标有什么特点？

在这里教师必须再次强调点的横坐标写在前面，纵坐标写在后面的坐标写法。

设计意图：先学一般点的坐标，再来探究特殊点的坐标，这样安排符合学生的学习规律，也更容易使学生理解和掌握。

3、点的坐标，

有了平面直角坐标系，平面内的点就可以用一个有序数对来表示了．如下图，由点A分别向x轴和y轴作垂线，垂足M在x上的坐标是3，垂足N在y轴上的坐标是4，有序数对(3，4)就叫做点A的坐标，其中3是横坐标，4是纵坐标．

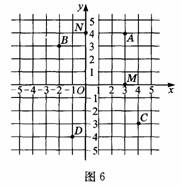
注意：表示点的坐标时，必须横坐标在前，纵坐标在后，中间用逗号隔开。

尝试：请在图6中写出点B、C、D的坐标。

设计说明：这一步是教学中的难点，教师一方面应强调点的坐标的书写规范，另一方面也必须安排一定的练习时间。

2、平面直角坐标系的概念

　　 教师边在黑板上画图(见教材第47页图6.1-4)，边介绍平面直角坐标系、x轴(或横轴),y轴(或纵轴)、原点等的概念．

　　 注意：在一般情况下，两条坐标轴所取的单位长度是一致的．

1、平面直角坐标系的引入

　　 对于上述第(2)个问题，我们可以用图3来表示： 这时，小兵(P)的位置就可以用两个数来表示．如点P离AB边1 cm，离AD边1. 5 cm，如果1 cm代表20 m，那么小兵离AB边20 m，离AD边30 m.

　　 对于上述第(3)个问题，我们是否也可以借助于这样的一些线来确定小兵的位置呢？我们在小兵所在的平面内画上一些方格线(如图4)，利用上节课所学的知识，就可以解决这个问题了．

(然后由学生回答这个问题的解决过程)

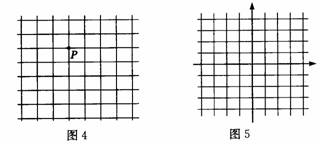
受上述方法的启发，为了确定平面内点的位置，我们可以画一些纵横交错的直线，便于标记每一条直线的顺序，我们又可以以其中的两条为基准(如图5).

　　 最早采用这种方法的是法国数学家笛卡儿，然后向学生简要介绍笛卡儿的有关故事．

2、如果我们画一条数轴，取小红的位置为原点，取向右的方向为正方向，取两盏路灯间的距离为一个单位长度，那么小华的位置(A)就可以用－3来表示，小明的位置(B)就可以用6来表示(如图2).此时，我们说点A在数轴上的坐标是－3，点B在数轴上的坐标是6．这样数轴上的点的位置与坐标之间就建立了对应关系．

设计意图：将数轴上点的坐标的概念学习置于具体的问题情境中。

　　 问题：(1)在上述情境中，如果小兵位于小明左侧的第二盏路灯处，你能说出小兵在数轴上对应的点的坐标吗？

　　 (2)如果小兵站在一个长方形的操场上，你用什么方法可以确定小兵的位置？

(3)如果小兵站在一个大操场上，你用什么方法可以确定小兵的位置？

设计意图：三个问题的安排有一定的层次性，为下一步引出平面直角坐标系作铺垫。

1、在一条笔直的街道边，竖着一排等距离的路灯，小华、小红、小明的位置如图1所示，你能根据图示确切地描述他们三个人的位置关系吗？

在学生进行叙述后，教师可以抓住以什么为“基准”，并借助于数轴来处理这个问题，从而进入课题．

设计意图：学生可以以其中的一人为基准进行描述，其目的是为数轴上的点的坐标的确定做准备。

3、备选题：

(1)如图10，下列说法中正确的是(　 )

　A　 点A的横坐标是4　 B 点A的横坐标是－4

　C　 点A的坐标是(4，－2) D 点A的坐标是(－2，4)

(2)下列说法中错误的是(　 )

　　 A　 x轴上的所有点的纵坐标都等 B　 y轴上的所有点的横坐标都等

　　 C　 原点的坐标是(0，0)　　 D 点A(2，－7)与点B(－7，2)是同一个点

[教学反思]

　 本教学设计立足于问题情境的创设，将原本枯燥的平面直角坐标系赋予一定的现实意义，在实际问题中学习知识，力求避免空洞的说教；立足于知识的发现和发展，让学生能在气种自然而然的情境中理解建立平面直角坐标系的必要性，应用平面直角坐标系去分析和解决问题；立足于知识和情感的教育，在知识教学的同时，结合数学家的故事及时地对学生进行理想教育，又在本课结束前对学生进行人生观的教育．同时在本设计中还力求体现学生探究能力的培养，通过一个个问题的设计，一步一步地引导学生进行探究及自主地进行学习，并及时地加以总结和反馈，尝试从多角度去体现新课程的教学理念．