活动一：教材第48页的“探究”．

　　 处理方法：先让学生独立尝试，然后小组内交流，最后教

师进行归纳：

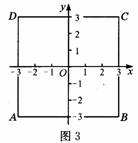
1、　 为了方便，我们一般以正方形的两条边所在的直线为坐标轴，建立平面直角坐标系(有四种情形)．另外，按图3的方式建立平面直角坐标系也是常用的．

4、例题：教科书第48页．

处理方法：先让学生尝试在方格纸上画图，然后教师根据巡视中发现的问题有针对性地进行讲解，使学生养成先找横坐标，再找纵坐标的习惯．同时突出两条垂线的交点才是所求的点的结论．

设计意图：这里可以根据学生的实际情况，先由教师示范，再让学生练习。

3、口答：分别说出下列各个点在哪个象限内或在哪条坐标轴上？

　　 A(6，－2)，B(0，3)，C(3，7)，D(－6，－3)E(－2，0)，

F(－9，5)]

设计意图：这里安排一组口答练习，是为了及时运用前面的规律，培养学生的空间想象能力；二是为下面例题的学习做准备。

2、探究点的位置与它的坐标的符号之间的关系．

　　 学生独立完成教材第50页的习题第2题的填表．然后分组讨论：

　 (1)四个象限内的点的坐标的符号有什么规律？

　 (2)从上表中你还能发现什么规律？

　　 最后归纳出一、二、三、四象限内点的坐标的符号分别是

(+，+)，(－，+)，(－，－)，(+，－)．同时还可以让学生说

出：x轴的正半轴上的点的横坐标为正数，纵坐标是零……

设计意图：通过学生自己的探究，既有利于对四个象限概念的理解，又有利于对点的坐标的理解。

1、象限的概念：

以教师讲解的方式介绍四个象限的概念，如图2

注意：坐标轴上的点不属于任何象限。

2、思考：

在上面的问题中，点B和点C的坐标之间有什么关系？每一个点的横坐标与纵坐标的符号与什么有关？

设计意图：设计这两个问题，一方面是复习上一节课的知识，一方面又为本节课的学习做准备．

　由于本节课是建立在上一节课的基础之上的，因此以复习的方式来引入新知的学习，也不失为一种好的方法。

1、在图1的平面直角坐标系、中，你能说出三角形ABC三个顶点A，B，C的坐标吗？

2、选做题：教材第51页习题6. 1的第8、10、11、12题

[教学反思]

　　 以探索活动贯穿整个课堂教学是本教学设计的一个特点．从探索各个象限内点的坐标的符号到探索同一个图形在不同的平面直角坐标系中坐标的变化，以及选择平面直角坐标系，都体现了学生的主体探究意识．在此基础上又进一步探究特殊点和它们的坐标之间的关系，这样安排的另一个目的也是为了开阔学生的思路和视野．由于本节课是建立在上一节课的基础之上的，因此在教学设计中也注意了教师的讲解与学生的自主学习之间的关系，使教师的讲解恰当、到位、有效．第三个特点是紧紧抓住了教材的重点，即在教学设计上始终突出点的位置与点的坐标之间的一一对应的关系．

1、必做题：教材第50页习题6.1的第5、6、7题．

3、你有什么收获？