2、归纳小结：

　　 在平面直角坐标系内，如果把一个图形各个点的横坐标都加(或减去)一个正数a，相应的新图形就是把原图形向右(或向左)平移a个单位长度；如果把它各个点的纵坐标都加(或减去)一个正数，相应的新图形就是把原图形向上(或

向下)平移a个单位长度．

设计意图：学生在观察、探究的基础上，归纳在直角坐标中图形的平移与坐标变化的规律，既让学生有一个充分从事数学活动的机会，又体现了学生是数学学习的主人的新理念．

1、思考：

　 (1)如果将引入问题中的“横坐标都减去6”“纵坐标都减

去5”，相应地变为“横坐标都加3”“纵坐标都加2"，分别能得

出什么结论？画出得到的图形．

　 (2)如果将三角形ABC三个顶点的横坐标都减去6，同

时纵坐标都减去5，能得出什么结论？画出得到的图形．

设计意图：在引入问题的基础上，让学生作出更深入的研究--纵横坐标都发生变化时，图形变化的规律，使学生亲身经历数学知识的形成过程。

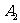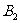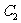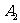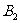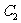2、将三角形ABC三个顶点的纵坐标都减去5，横坐标不变，分别得到、、依次连接、、各点，所得三角形

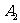
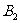
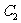与三角形ABC在大小、形状和位置上有什么关系？

如图1，三角形ABC三个顶点的坐标分别为

A(4，3)，B(3，1)，C(1，2)．

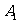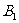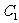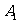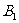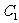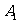
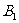
1、将三角形ABC三个顶点的横坐标都减去6，纵坐标不变，分别得到点、、，依次连接、、各点所得的三角形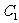,与三角形ABC在大小、形状和位置上有什么

关系？

2、选做题：教科书60页第6题．

[教学反思]

　本课创设了在学生已有的知识经验基础之上的情境，能激发学生学习的积极性．学生通过在直角坐标系下坐标的平移与点的坐标变化规律的探索，亲身经历了知识的形成过程．不但改变了以往学生死记硬背的学习方式，而且在教学活动中培养了学生自主探究、合作交流等良好的学习习惯．学生在观察、探究的基础上归纳出在平面直角坐标中，点的平移与坐标变化的规律，这既给学生提供了一个充分从事数学活动的机会，又体现了学生是数学学习的主人的理念．本课的教学过程设计为：情境－问题－探究－反思(归纳)－提高，这充分体现了新课程理念下，数学课堂教学方式的根本转变．

1、必做题：教科书59页习题6.2第2、冬4题．

练习：1、如图2，△AOB沿x轴向右平移3个单位之后，得到△A'B'C'，则△A'B'C'的三个顶点坐标为多少？

2、如图3, △AOB关于x轴对称图形△A'OB，则对应顶点的坐标有什么变化？

设计意图：学生通过课堂练习，能够更好的理解新知，巩固新知。

2、归纳：在直角坐标系中，将点(x，y)向右(或向左)平移a个单位长度，可以得到对应点(x+a，y)或[(x-a，y)]，将点(x,y)向上(或向下)平移b个单位长度，可以得到对应点(x，y+b)[或(x，y一b)]．

设计意图：由学生归纳平面直角坐标系中点的平移与坐标变化规律，给他们提供了一个充分从事数学活动的机会，也体现了学生是数学学习的主人．

1、探究：把△ABC向左(或向上)平移3个单位，相当于把△ABC的三个顶点坐标A(1，1)，B(3，1)，C(4，3)分别向左(或向上)平移了3个单位得到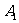、、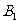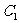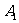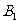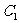，、、三点坐标分别为多少？

设计说明：通过学生合作交流，教师参与引导学生得出，直角坐标系中图形的平移实质是点的平移及点平移后坐标的变化的规律。

如图1, △ABC的三个顶点坐标分别为A(1，1)，B(3，1),C(4,3)，把△ABC向左(或向上)平移3个单位后，顶点A，B，C的坐标分别为多少？

设计意图：创设在学生已有的知识经验基础之上的情境，引入新知，能激发学生的学习兴趣，既复习了旧知识，又引出了本课学习内容，起到承上启下的作用。