
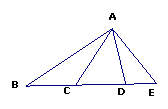
5、如图,以点A为以点一个端点的线段有多少条?以点B为一个端点的线段有多少条、请分别表示这些线段;图中共有多少个三角形?
4、 如图,图中能用字母表示的
如图,图中能用字母表示的
直线是: ;
 射线是:
;
射线是:
;
线段是: 。
3、一条直线上取三个点,最多可以确定 条射线。
2、如图估测线段AB与线段BC的大小关系,再用刻度尺或圆规来检验你的结论

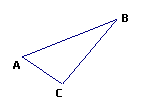
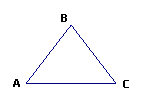
2、线段、射线、直线的表示:

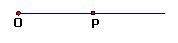
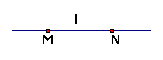
请你用符号表示出上面的线段、射线、直线
线段: ;射线: ;直线: ;
完成下表:
|
名 称 |
图形及表示方法 |
不 同 点 |
联 系 |
共同点 |
||
|
延伸情况 |
端点数 |
与实物联系 |
||||
|
线 段 |
|
|
|
|
|
|
|
射 线 |
|
|
|
|
||
|
直 线 |
|
|
|
|
讨论:如图,点B、C在线段AD上

(1)图中以A为一个端点的线段有几条?以B为一个端点的线段有几条?
(2)图中共有多少条线段?请分别表示出这些线段。
 练习:1、如图,一张长方形的纸片
练习:1、如图,一张长方形的纸片
(1)量一量,“长”比“宽”长了多少?
(2)用折纸的方法比较“长”与“宽”的大小。
1、讨论:①如图所示,从甲地到乙地有三条路,走哪条路相对近一些?

②从甲地到乙地能否修一条最短的路?如果能,你认为这条路应该怎样修,请在图中画出这条路。
得出的结论是: 。
定义:两点之间的距离: 。
“线段”和“两点之间的距离”的区别: 。
2、布置作业:
(1)必做题:教材60页第7、8题.
(2)选做题:教材61页第9题.
(3)备选题:
在平面直角坐标系中,将坐标为(0,0),(2,4),(2,0),(4,4)的点用线段依次连接起来形成一个图案:
①这四个点的纵坐标若保持不变,横坐标变成原来的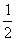 ,将所得的四个点用线段依次连接起来,所得的图案与原图案相比有什么变化?
,将所得的四个点用线段依次连接起来,所得的图案与原图案相比有什么变化?
②纵坐标保持不变,横坐标分别加3呢?
③横坐标不变,纵坐标分别加3呢?
④纵坐标保持不变,横坐标分别变为原来的2倍呢?
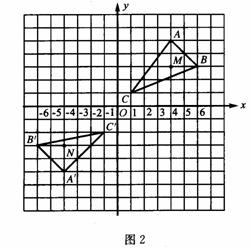
如图2,三角形A'B'C'是三角形ABC经过某种变换后得到的图形,分别写出点A与点A',点B与点B',点C与点C'的坐标,并观察它们之间的关系,如果三角形中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么?
[教学反思]
本课的教学设计思路为:情境-问题-探究-反思-提高.在整个教学过程中,无论是从情境中引入,还是对新知的探究及拓广,始终体现了学生作为数学学习的主人作用,教师起到了一个合作者、组织者、引导者的作用.建构主义教学理论认为:学习总是与一定的问题情境相联系的.本课从新知的引入到新知的拓广都是以问题的形式呈现给学生,这样不但能激发学生的学习积极性,而且也为学生主动建构新知提供了保证.本课学生通过对平面直角坐标系下图形的平移与坐标变化的规律探索,使学生更深人体会到平面直角坐标系的作用,也体现了数学活动充满创造与探索的魅力.
1、课堂练习:教材58页练习.
2、如果将△ABC三个顶点的横坐标和纵坐标都乘2,画出得到的图形,并分析新图形与原图形又有何关系.
设计意图:通过对坐标问题的拓广,把学生的思维引领到更为广阔的领域,同时使学生更深刻领会坐标变化与图形变化的关系。
1、问题:如果将引人问题中的△ABC三个顶点的横坐标都乘2,画出得到的图形,说出它与原图形有何关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com