4．教学目标　　

◆认知目标

(1)掌握二次函数 y=ax2+bx+c图像与系数符号之间的关系。

通过复习,掌握各类形式的二次函数解析式求解方法和思路,能够一题多解,发散提高学生的创造思维能力.

◆能力目标

提高学生对知识的整合能力和分析能力.

◆ 情感目标　

制作动画增加直观效果,激发学生兴趣,感受数学之美.在教学中渗透美的教育，渗透数形结合的思想，让学生在数学活动中学会与人相处，感受探索与创造，体验成功的喜悦。

3．学情分析

(1)初三学生在新课的学习中已掌握二次函数的定义、图像及性质等基本知识。

(2)学生的分析、理解能力较学习新课时有明显提高。

(3)学生学习数学的热情很高，思维敏捷，具有一定的自主探究和合作学习的能力。

(4)学生能力差异较大，两极分化明显。

2．课标要求：

①通过对实际问题情境的分析确定二次函数的表达式，并体会二次函数的意义。

②会用描点法画出二次函数的图象，能从图象上认识二次函数的性质。

③会根据公式确定图象的顶点、开口方向和对称轴(公式不要求记忆和推导)，并能解决简单的实际问题。

④会利用二次函数的图象求一元二次方程的近似解。

1．地位和作用　

(1)函数是初等数学中最基本的概念之一，贯穿于整个初等数学体系之中，也是实际生活中数学建模的重要工具之一.二次函数在初中函数的教学中有重要地位，它不仅是初中代数内容的引申，也是初中数学教学的重点和难点之一,更为高中学习一元二次不等式和圆锥曲线奠定基础。在历届淮安市中考试题中，二次函数都是不可缺少的内容。

(2)二次函数的图像和性质体现了数形结合的数学思想，对学生基本数学思想和素养的形成起推动作用。

(3)二次函数与一元二次方程、不等式等知识的联系，使学生能更好地将所学知识融会贯通.

6.2角(2)

题目 6.2角(2) 教学目标 会利用三角尺、圆规、量角器、直尺等画图工具画一个角等于已知角 在操作活动中理解角平分线的概念，并会进行简单的计算 教学重点 利用绘图工具画一个角等于已知角 教学难点 尺规作图画一个角等于已知角 理解角平分线的概念 教学方法 引导发现式 教学工具 三角尺、圆规、量角器 教学内容 教师活动 学生活动

一些特殊的角度我们可以用一副三角尺画出 例如∠AOB=45°+30°＝75° ∠AOB=45°－30°＝15° 　 　 　 　 说明：0°到180°之间的所有15°的整数倍角都可以用三角尺画出 用量角器可以画出0°到180°之间任意角度 尺规作图画一个角等于已知角 1.　　　 以点O为圆心，任意长为半径用圆规画弧，分别交OA、OB于点C、D 2.　　　 任意画一点O画射线OA，以点O为圆心，OC长为半径画弧CE，交OA于点C 3.　　　 以点C为圆心，CD长为半径画弧，交弧CE于点D 4.　　　 B 　 过点D作射线OB，∠AOB就是与∠AOB相等的角 O 　 OC将∠AOB分成相等的两部分，OC就是∠AOB的角平分线 我们还可以得到： 如果OC是∠AOB的角平分线 则∠AOC＝∠BOC＝∠AOB 反过来如果∠AOC＝∠BOC或者∠AOC＝∠AOB，　 ∠BOC＝∠AOB 则OC是∠AOB的角平分线 O 　 例 　 ∠AOD＝80°，OB是∠AOC的角平分线， ∠AOB＝30°试求∠AOC、∠COD的度数 解：∠AOC＝2∠AOB＝2×30°＝60° ∠COD＝∠AOD－∠AOC=80°－60°＝20° 练习： P208 1、2 作业： P209 3、4

3、能借助圆规作一条线段等于已知线段。

作　　 业：P125习题4.2：1。

教学后记：学生能判断两点之间的所有连线中线段最短，但不会说，说明他们的表达能力较差。大部分同学会用圆规作一条线段等于已知线段。理解线段的中点是平分线段的，但在解决实际问题中，不会用字母表示中点的性质。

3、线段的中点：

点M把线段AB分成相等的两条线段AM与BM，点M叫做线段AB的中点，即AM＝BM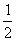＝AB

小　　 结：1、理解“两点之间的所有连线中，线段最短”的性质；

2、如何比较两条线段AB与CD的长短？

一种方法是把它们放在同一条直线上比较；

画一条直线l，在l上先作线段AB，再作出线段CD，并使点C与点A重点，点D与点B位于点A的同侧。

(1)　　 如果点D与点B重合，就说线段AB与线段CD相等，记作AB＝CD

(2)　　 如果点D在线段AB内部，就说线段AB大于线段CD，记作AB＞CD

(3)　　 如果点D在线段AB外部，就说线段AB小于线段CD，记作AB＜CD

另一种方法是用刻度尺量出线段AB与线段CD的长度，再进行比较。

练习：P125随堂练习：1、2

1、用圆规作一条线段等于已知线段：先作一条射线AB，用圆规量出已知线段的长度(记作a)，再在射线AB上以A为圆心，截取AC＝a

2、能用圆规作一条线段等于已知线段。

教学难点：用圆规作一条线段等于已知线段。

教学方法：尝试练习法、观察发现法、比较法。

教学用具：多媒体教学平台。

活动准备：

放映图片：从图片说明“两点之间的所有连线中，线段最短”的性质。

引出――比较线段的长短

教学过程：