1、抛物线y=﹣2(x﹣3)²﹢5的开口　　 　,对称轴是　　　 　, 顶点坐标为　　　　 　,当x　　 　,y随x的增大而增大; 当x　　 　, y随x的增大而减小；当x=　　 　，y最　　　 值为　　　 　　.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　2、将抛物线 y=x² 向　　　 　平移　　　 个 单位,再向　　 平移　 个单位,就可得y=x²-4x-4.

5.二次函数y=ax²+bx+c的对称轴为x=-b/2a，最值为y=　　 　　　,　 要善于利用图象的对称性,同时抓住抛物线的顶点、与x轴的交点，与y轴的交点这几个关键点来解决有关的问题。

4.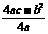常用的二次函数解析式的求法

3. 抛物线与x轴交点个数的判定

2.抛物线y=ax²+bx+c的特征与a、b、c的符号：

(1)a决定开口方向:

(2)a与b决定对称轴位置:

(3) c决定抛物线与y轴交点位置

1.一般地，y=ax²+bx+c(a,b,c是常数，a≠0)称为y是x的二次函数，它的图象是抛物线. 　

本节课的设计，我以学生活动为主线，通过“观察、分析、探索、交流”等过程，让学生在复习中温故而知新，在应用中获得发展，从而使知识转化为能力。本节教学过程主要由创设情境，引入新知――合作交流；探究新知――运用知识，体验成功；知识深化――应用提高；归纳小结――形成结构等环节构成，环环相扣，紧密联系，体现了让学生成为行为主体即“动手实践、自主探索、合作交流“的《数学新课标》要求。本设计同时还注重发挥多媒体的辅助作用，使学生更好地理解数学知识；贯穿整个课堂教学的活动设计，让学生在活动、合作、开放、探究、交流中，愉悦地参与数学活动的数学教学。

(四)方法与小结

由总结、归纳、反思，加深对知识的理解，并且能熟练运用所学知识解决问题．

2、作业设计：(见课件)

3、板书设计：(见课件)

(三)综合应用能力提高

既培养学生运用知识的能力，又培养学生的创新意识。引导学生对学习内容进行梳理，将知识系统化，条理化，网络化，对在获取新知识中体现出来的数学思想、方法、策略进行反思，从而加深对知识的理解。并增强学生分析问题，运用知识的能力。

(二)典型例题分析

通过反馈使学生掌握重点内容。