上述函数函数关系有哪些共同之处？它们与一次函数、反比例函数的关系式有什么不同？

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 .

一般地，形如　　　　　　　　 ，(　 　　　　　　，且　　　 )的函数为二次函数.其中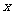是自变量，　　　　　　　 函数.

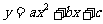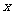一般地，二次函数中自变量的取值范围是　　　　　　　　 ，你能说出上述三个问题中自变量的取值范围吗？

3．要给一个边长为x (m)的正方形实验室铺设地板，已知某种地板的价格为每平方米240元，踢脚线价格为每米30元，如果其它费用为1000元，那么总费用y(元)与x(m)之间的函数关系式是　　　　　　　　 　　　　　　　　　　　　.

2．用16m长的篱笆围成长方形圈养小兔，圈的面积y(㎡)与长方形的长x(m)之间的函数关系式为　　　　　　　 　　　　.

1．一粒石子投入水中，激起的波纹不断向外扩展，扩大的圆的面积S与半径r之间的函数关系式是　　　　　　　 　　　　.

3. 形如，(　　　　　　　 )的函数是一次函数，当时，它是　　　　　　　　 函数，图像是经过　　　　 的直线；形如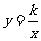，(　　　　 　　　)的函数是　　　　　 函数，它的表达式还可以写成：①　　　　　　　 、②　　　　　　　 .

2.我们已经学过的函数有：一次函数、反比例函数，其中　　　　　　　 的图像是直线，

　 　　　　　　　　的图像是双曲线.我们得到它们图像的方法和步骤是：①　　　　　　 、

②　　　　　　　 、③　　　　　　　　 .

1.设在一个变化过程中有两个变量x和y，如果对于x的每一个值， y都有唯一的值与它对应，那么就说y是x的　　　 ，x叫做　　　　　　 .

3.要准确辨析条件，选用适当的形式求二次函数解析式。如：(1)已知顶点坐标、对称轴或最值常可选用顶点式；(2)从问题情境出发，确定二次函数解析式。

(4)通过计算(或运用二次函数性质)确定二次函数中的有关量。

2.二次函数还与一元二次方程的知识紧密联系.利用方程根的性质、根的判别式，可判定抛物线与x轴交点的情况；反之，可以求某些字母的取值范围.

1.二次函数的图象有着丰富的内涵,解决二次函数的题目应尽可能地画出大致的抛物线图象,结合图形,解决问题.利用a、b、c的值可判断二次函数的大致位置情况；反之，若已知二次函数的大致位置，也可以判断出一些特殊关系式或a、b、c的取值范围等.