
4、二次函数的定义
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.
注意:定义中只要求二次项系数a不为零(必须存在二次项),一次项系数b、常数项c可以为零。最简单形式的二次函数-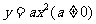
例如,y=-5x2+100x+60000和y=100x2+200x+100都是二次函数.我们以前学过的正方形面积A与边长a的关系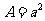 ,圆面积s与半径r的关系
,圆面积s与半径r的关系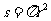 等也都是二次函数的例子.
等也都是二次函数的例子.
3、做一做
银行的储蓄利率是随时间的变化而变化的。也就是说,利率是一个变量.在我国利率的调整是由中国人民银行根据国民经济发展的情况而决定的.
设人民币一年定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存.如果存款额是100元,那么请你写出两年后的本息和y(元)的表达式(不考虑利息税):
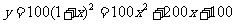 .
.
如果考虑利息税,那么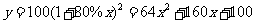 .
.
2、想一想
在上述问题中,种多少棵橙子树,可以使果园橙子的产量最多?
我们可以列表表示橙子的总产量随橙子树的增加而变化情况.你能根据表格中的数据作出猜测吗?自己试一试.
|
x/棵 |
8 |
9 |
10 |
11 |
12 |
|
y/个 |
60480 |
60495 |
60500 |
60495 |
60480 |
从表格中发现:增种10棵橙子树时,橙子的总产量最多.
1、由实际问题探索二次函数
某果园有100棵橙子树,每一棵树平均结600个橙子,现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)问题中有哪些变量?其中哪些是自变量?哪些因变量?
(2)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
果园共有(100+x)棵树,平均每棵树结(600-5x)个橙子,因此果园橙子的总产量
y=(100+x)(600-5x)=-5x2+100x+60000.
提出问题:判断上式中的y是否是x的函数?若是,与我们前面所学的函数相同吗?(根据函数的定义,y是x的函数,从形式上看不同于我们所学函数,猜测是二次函数)
回忆学过的函数类型-一次函数(正比例函数)、反比例函数、三角函数;函数定义-在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.本节课我们将开始教学初中阶段的最后一个函数二次函数.
6.已知函数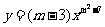 是二次函数,求m的值.
是二次函数,求m的值.
4. 如图在长200米,宽80米的矩形广场内修建等宽的
十字形道路,请写出绿地面积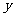 (㎡)与路宽
(㎡)与路宽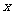 (m)之间
(m)之间
的函数关系式: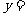 .
.
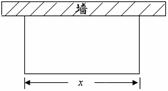 5. 如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积
5. 如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积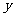 (㎡)与它与墙平行的边的长
(㎡)与它与墙平行的边的长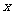 (m)之间的函数
(m)之间的函数
关系式: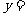 .
.
2.若一个边长为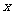 cm的无盖正方体形纸盒的表面积为
cm的无盖正方体形纸盒的表面积为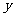 cm
cm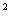 ,则
,则 ,其中
,其中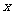 的取值范围是
.
的取值范围是
.
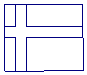 3.一矩形的长是宽的1.6倍,则该矩形的面积
3.一矩形的长是宽的1.6倍,则该矩形的面积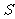 与宽
与宽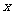 之间函数关系式:
之间函数关系式: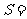 .
.
1.考察下列函数:①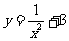 ,②
,②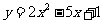 ,③
,③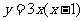 ,④
,④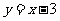 ,
,
⑤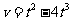 (
(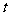 是自变量)中,二次函数是:
.
是自变量)中,二次函数是:
.
例1.当k为何值时,函数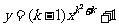 为二次函数?
为二次函数?
例2.写出下列各函数关系,并判断它们是什么类型的函数.
⑴圆的面积y(cm2)与它的周长x(cm)之间的函数关系;
⑵某种储蓄的年利率是1.98%,存入10000元本金,若不计利息,求本息和y(元)与所存年数x之间的函数关系;
⑶菱形的两条对角线的和为26cm,求菱形的面积S(cm2)与一对角线长x(cm)之间的函数关系.
例3.已知二次函数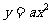 ,当
,当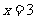 时,
时,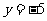 .当
.当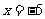 时,求
时,求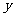 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com